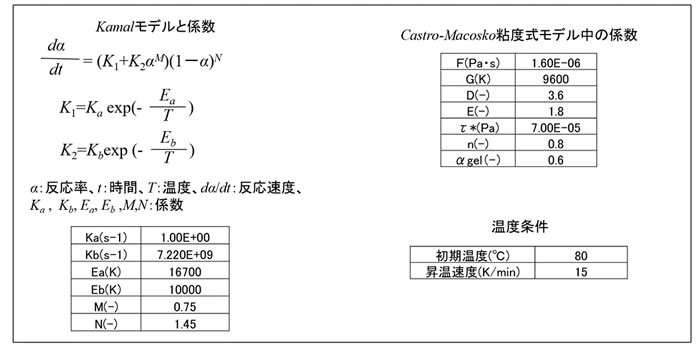
樹脂成形とレオロジー 第17回「 熱硬化性樹脂の粘度式モデル」

熱硬化性樹脂は反応の進行に伴い分子間の結合が進み分子は動きにくくなるので粘度が指数関数的に増大し、ゲル化点で液体から固体へと変化します。これにせん断速度と温度の影響が加わりますので、実際の成形工程では非常に複雑な粘度変化をします。ここでは、CAEでよく用いられているCastro-Macosko粘度式モデルについて説明します。
Castro-Macosko 粘度式モデル
このモデル式を(1)~(3)式にまとめました。(1)式は硬化反応による粘度上昇式、(2)式は粘度のせん断速度依存式、(3)式は粘度の温度依存式という三段構えの構成になっています。以下、それぞれの式について解説していきます。


硬化反応による粘度上昇式
(1)式をηmで除すると次の無次元式が得られます。いま、せん断速度と温度が一定の場合を考えます。このときηmは定数になります。
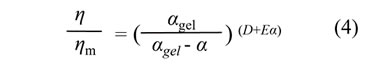
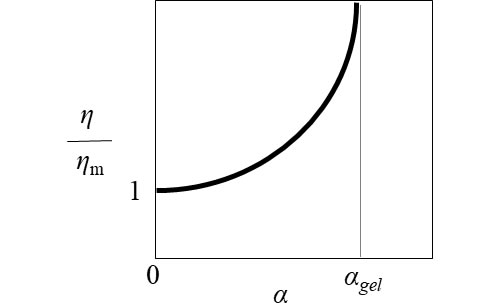
ηmを一定としたときの (4)式の特性値を図1に示します。反応率α=0で無次元粘度は1になり、αの増加とともに値が指数関数的に増加します。αがゲル化反応率αgelに達したときに右辺の分母が0になりますので粘度が∞に達します。なお、(1)式は反応率の情報が必要になります。これは前回ご説明したKamalモデルを使って与えられた条件下での反応率の計算を別途行っておき、得られた値を逐次(1)式に代入して計算を進めるという方式が一般的です。
![]()
粘度のせん断速度依存式
(2)式はCrossモデルとよばれ、熱可塑性樹脂のCAEでもよく使われています。(2)式を見やすくするため、次のようにしてみます。
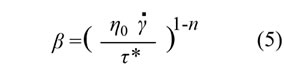
(2)式は次の形になります。
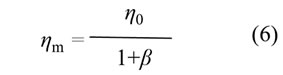
![]()
このときはβが0に近づきますので次式が得られます。
![]()
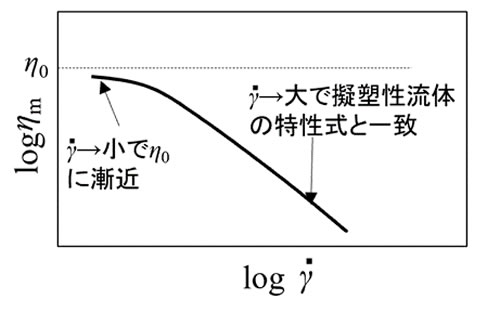
すなわち、ひずみ速度が小さくなるにしたがって、η0に漸近していきます。
![]()
このときはβが非常に大きくなり(6)式の分母の1は無視できますので次式が得られます。
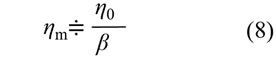
元の記号を使って整理すると次式が得られます。
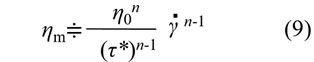
ここで次のようにしてみます。
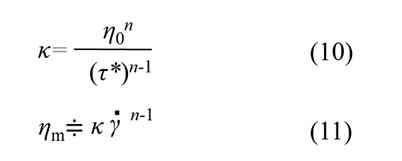
これは以前ご説明した擬塑性流体の特性式と同じ形になります。
粘度のせん断速度依存式は反応率と温度を固定すると図2の特性になります。
![]()
粘度の温度依存式
これは以前にご説明したアンドレードの式の形になっています。温度が高いほどη0が低下します。なお、基準温度でのη0を決めておき、温度と温度シフト因子の関係をWFLモデル式で表して任意温度でのη0を求める方法もあります。(第10回:「粘度の温度依存性の表わし方」参照)
計算例
ここでは反応速度式にKamalモデルを用い、Castro-Macosko粘度式モデルと組み合わせた計算例を紹介します。表1のように係数と温度条件を与えます。
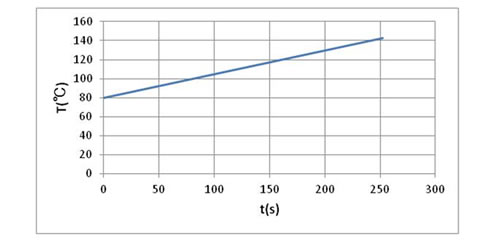
一定昇温条件ですので、温度は図3のように変化します。
![]()
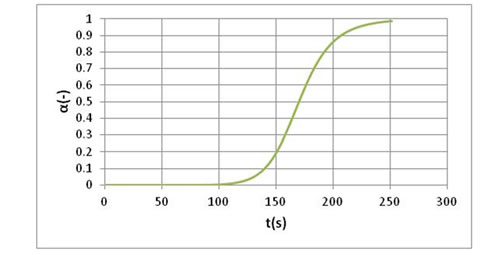
図4に反応率の変化を示します。時間の経過とともに反応率は増加し、250s程度で反応率が1に達し、反応が終了します。ここではゲル化反応率を0.6に設定していますので175s程度で樹脂がゲル化することになります。
![]()
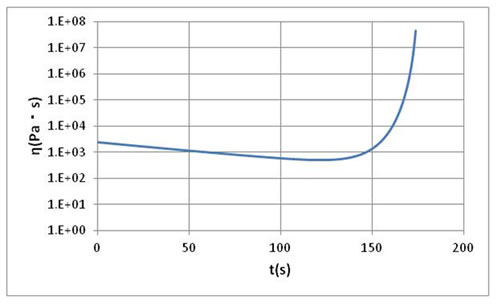
図5に粘度変化を示します。ここではせん断速度は1000s-1に固定しています。最初は時間の経過とともに粘度が低下し、途中から粘度上昇してゲル化時間で粘度が無限大になります。昇温過程では温度上昇による粘度低下と反応の進行による粘度増加が同時に起きており、初期では前者の寄与が大きく、後半に後者の寄与が支配的になるため、図5のような粘度変化となります。
![]()
補足事項:
粘度のせん断速度依存性がCrossモデルの形に従わない材料の場合は、その特性に合うモデル式の形の構築が必要です。
関連記事/関連ページ
●樹脂成形とレオロジー 第16回 「Kamalの反応速度モデル」
●樹脂成形とレオロジー 第18回 「伸長流動について」