樹脂成形とレオロジー 第20回「 K-BKZモデルについて」
K-BKZモデル
伸長流動挙動を含めて、粘弾性体のCAE解析用にもっともよく使われているのが、積分型構成方程式のK-BKZモデルです。 基本形は(1)式で、その構成要素の一部が(2)式と(3)式になります。また、温度依存性を表すときは(2)式が(4)式の形になり、その構成要素の一部が(5)式と(6)式になります。 (1)式が積分形になっているのは、現在の応力は過去の時刻におけるひずみの現在までの履歴で決まることを示しています。これらの式も記号の意味も大変わかりにくいですが、ここではできるだけ単純な現象に限定して原理を説明してみたいと思います。なお、ひずみテンソルと不変量については専門書などを参考にして下さい。
記憶関数mの役割
ここで現象を単純化するため、(2)式でN=1として一組のGとτの組み合わせのみとします。そして、記憶関数mを時刻0からtまで積分し、その値をモジュラスF(t)とします。
![]()
これはVoigtモデルで一定応力下でのクリープ流動の解と同じ形になります*。一方、通常の緩和モジュラスG(t)はMaxwell モデルにより下式となります*。
*連載第5回「粘弾性体のモデル化」参照
![]()
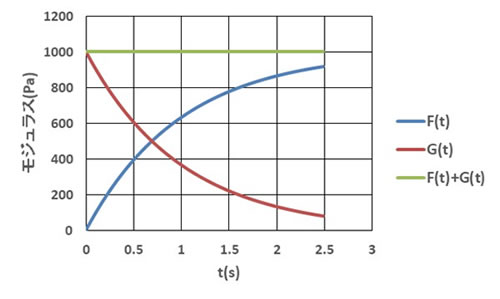
各モジュラスの時間変化例を図1に示します。 F(t)はGに向けて漸近し、 G(t)は0に向けて漸近します。両者の和は常にGの値になります。ある時刻におけるG(t)にその時までに生じたひずみを乗じると発生応力が出ます。 G(t)は過去の履歴によらず応力を求められるモジュラスなので積分は必要としません。一方、 F(t)はクリープ流動の解との類似性から、流動中の挙動に起因する応力を求める役割を担っていると考えられます。このときはひずみの時間変化であるひずみ速度の履歴が必要となるので(1)式のような積分形となります。
伸長流動の場合は、m(t)を用いた流動挙動起因の応力と、 G(t)ならびにその時点でのひずみ量を用いた応力との合計が材料に発生する総応力となります。
![]()
減衰関数hの役割
![]()
ここで、α:試料にせん断ひずみを与える実験から得られる係数、β:一軸または二軸伸長の実験から求められる係数です。通常、α>3、0<β<1の大きさになることが多いようです。一軸伸長のとき、I1、I2は伸長比λ(現在の長さを初期長さで除した値) を用いて次式となります。
![]()
![]()
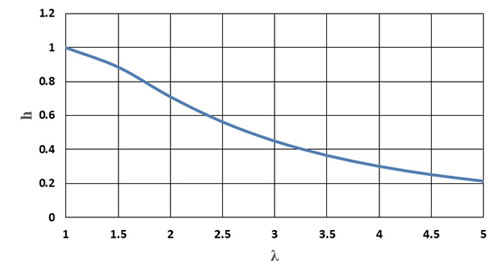
一軸伸長のときのλとhの関係例を図2に示します。hは試料が伸ばされるほど値が減少していきます。減衰関数はひずみが大きいほど緩和モジュラスが減少するという実現象に基づいています。また、hを表す色々なモデル式が存在しますが、今のところPMSとよばれる(3)式が標準的になっています。
![]()
FingerひずみテンソルC -1
これは変形モードにより決まり、一軸伸長のとき次式となります。
![]()
ここで、添え字の11は伸長方向、22はその直交方向を示します。
ひずみ速度![]() とλの関係
とλの関係
ひずみ速度が一定の時、次式の関係が得られます。したがって、hやC -1はひずみ速度と時間の関数に置き換えられます。
![]()
一定ひずみ速度での一軸伸長粘度計算式
以上をまとめますと、一定ひずみ速度での一軸伸長粘度計算式は次のようになります。ここでは発生応力をひずみ速度で除して粘度の単位にしてあります。なお、これまで一軸伸長粘度はηEで表してきましたが、計算で求めるときは一般的に右肩に+を付けることが多いので、これ以降は ηE +とします。
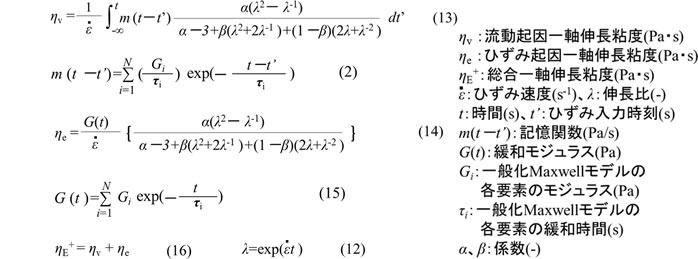
参考:単純せん断流動での粘度の計算式
この場合の粘弾性流体の粘度は下式となります(式の導出は省略)。係数βは存在しませんが、積分の部分と積分を行わない部分の足し合わせの形は一軸伸長粘度計算式と同じになります。(17)式は一軸伸長粘度との比較用に使います。
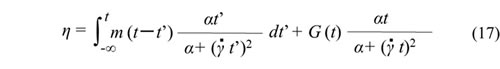
![]()
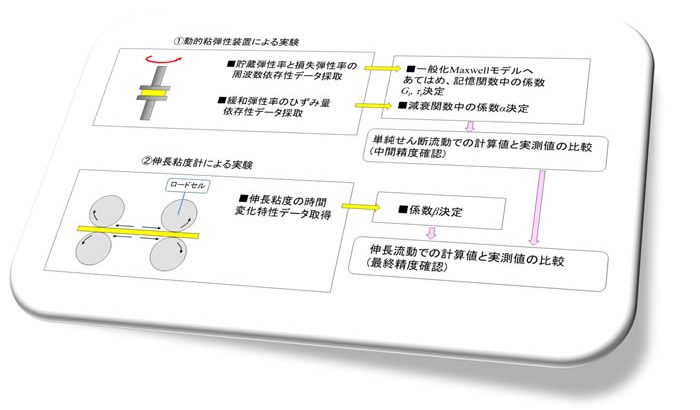
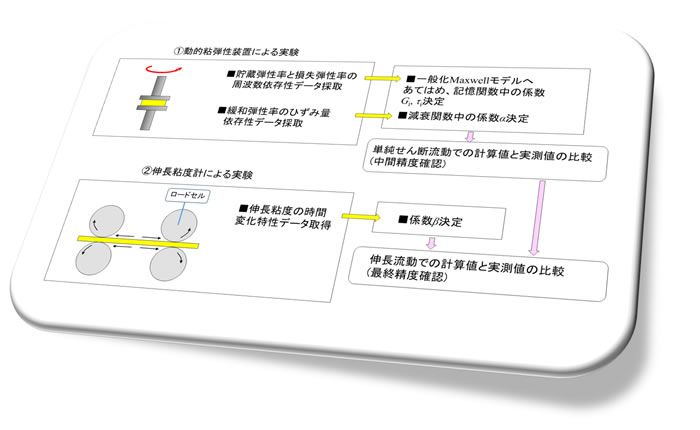
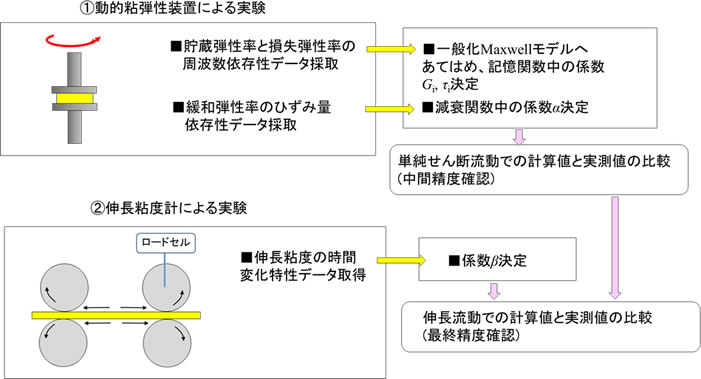
備考:K-BKZモデル式中の係数の決定手順の例
係数の値は次のような各種実験により求めるのが一般的です。
次回は係数を与えたときの具体的な計算例を示します。
関連記事/関連ページ
●樹脂成形とレオロジー 第19回 「伸長粘度の測定法と特性例」
●樹脂成形とレオロジー 第21回 「K-BKZモデルでの伸長粘度の計算例」