樹脂成形とレオロジー第24回「樹脂の周波数依存特性の一般化Maxwellモデルへの変換」
今回は、動的粘弾性装置で得られる周波数依存特性値を一般化モデルに置き換える例についてご紹介します。
樹脂の周波数依存特性例
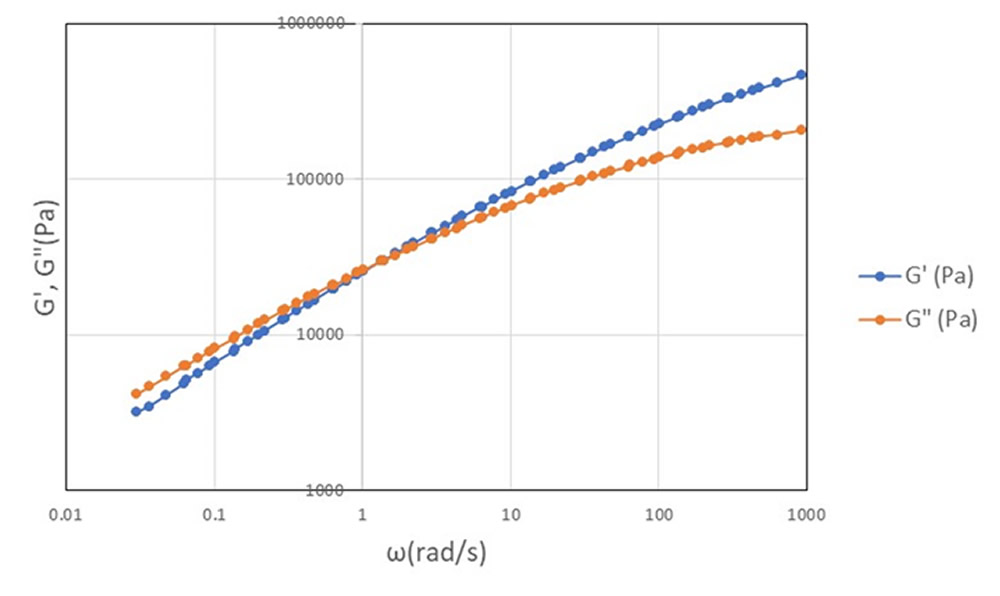
ある温度における材料Aの周波数依存特性値を図1に示します。角周波数 \(\omega\) が小さいときには貯蔵弾性率 G’ が損失弾性率 G” よりも小さいですが、 \(\omega\) =1rad/s 付近で値が重なり、その後は G’ の方が G” よりも大きくなります。これは前回ご紹介した特性通りになっています。
![]()
一般化Maxwellモデルへの変換式
緩和弾性率の表現方法は弾性体に粘性の寄与を考慮した構造解析の分野と、粘性体に弾性の寄与を考慮した樹脂流動解析の分野で異なっており、その違いを説明します。
構造解析の分野では、純弾性特性を表現するばね単独要素があり、これに並列に二要素Maxwellモデルが並びますので次式の形になります。これをプロニー級数と称しています。
![]()
ここで、G :緩和弾性率、t :時間、G∞ :ばね単独要素の弾性率、N :二要素Maxwellモデルの列数、Gi :各列の弾性率、 \(\lambda\)i :各列の緩和時間です。
一方、粘性特性を有する樹脂流動解析では粘性項を含まないばね単独要素は使いませんので、通常は次式の一般化Maxwellモデルを用います。
![]()
(2)式を基準としてばね単独要素を加えた場合はZenerモデルと呼ばれ、プロニー級数と同じになります。なお、(2)式のままでも一つの項の \(\lambda\) を非常に大きくしておけば、その項はばね単独要素の役割を果たせますので、特に(1)式の形にする必要はありません。したがって、ここでは(2)式の一般化Maxwellモデルを用いることにします。
一方、動的粘弾性装置での実験により得られる G’ 、 G” とCAE解析で用いる一般化Maxwellモデル中の係数 Gi , \(\lambda\)i (緩和スペクトル)の関係は次式となります。
![]()
![]()
(3)、(4)式に図1の各ポイントで得られる G’ 、G” とそのときの \(\omega\) の値を代入すると、 Gi 、 \(\lambda\)i を未知数とする連立方程式が並びます。この形は代数的に解けませんので、全体の誤差が最小になるように近似解を求めることになります。
緩和スペクトルの値の決定
ここでは、なめらかな非線形関数での最適解を求めるのに適したGRG(Generalized Reduced Gradient)非線形ソルバー1)を用い、 N=6の一般化Maxwellモデルでの係数を最適化してみました。
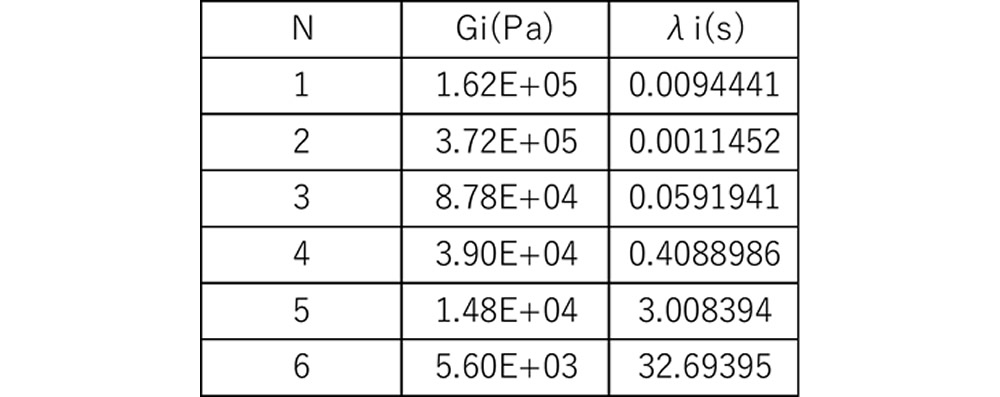
結果を表1に示します。G が大きい列では \(\lambda\) が小さく、G が小さくなると \(\lambda\) が大きくなる組み合わせになっています。
![]()
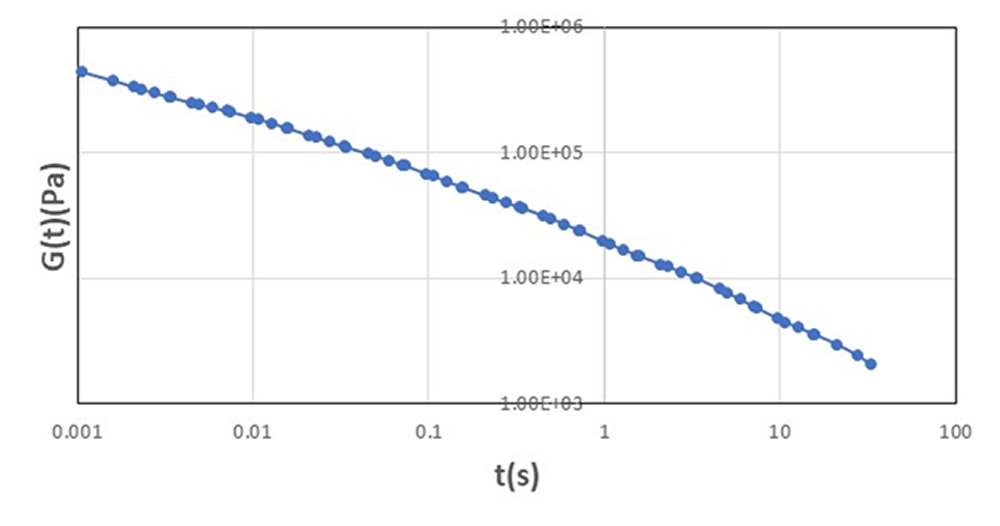
このときの緩和弾性率曲線を図2に示します。時間の経過とともに弾性率 G(t) がなめらかに小さくなっていきます。
![]()
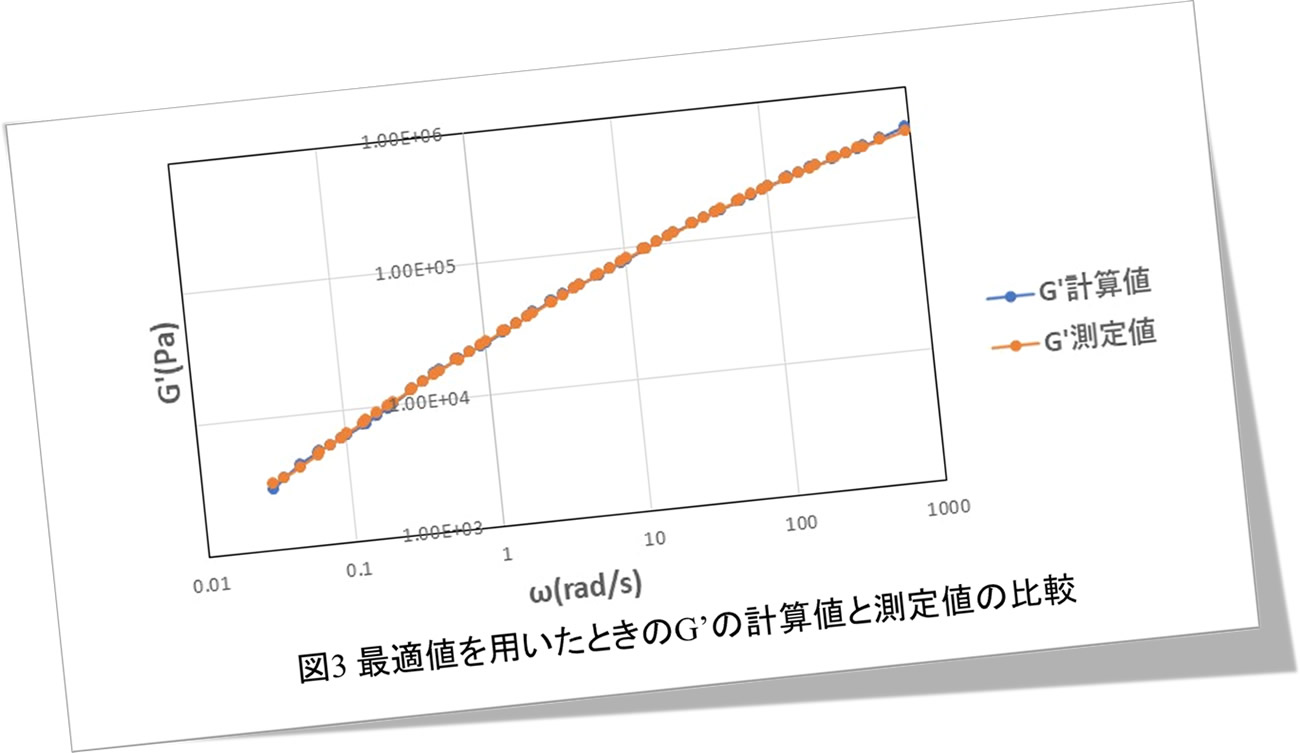
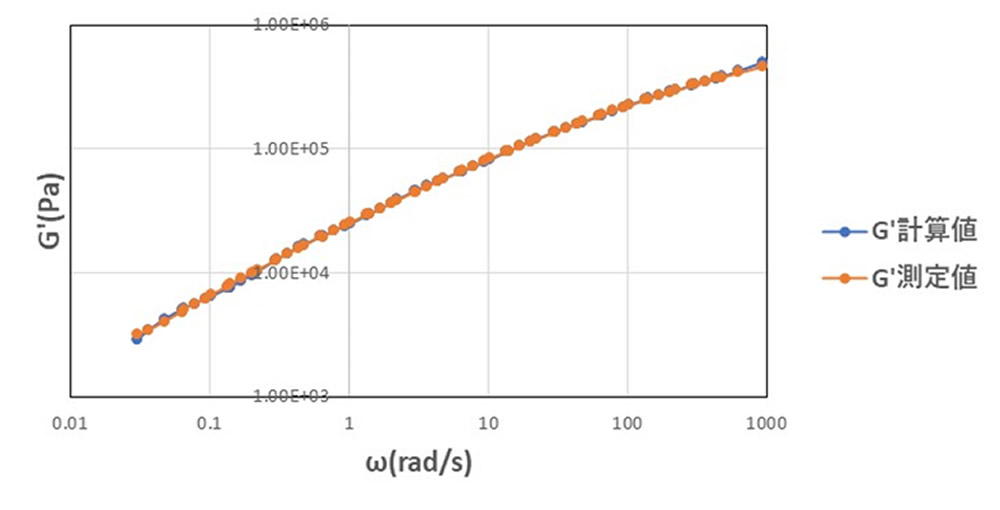
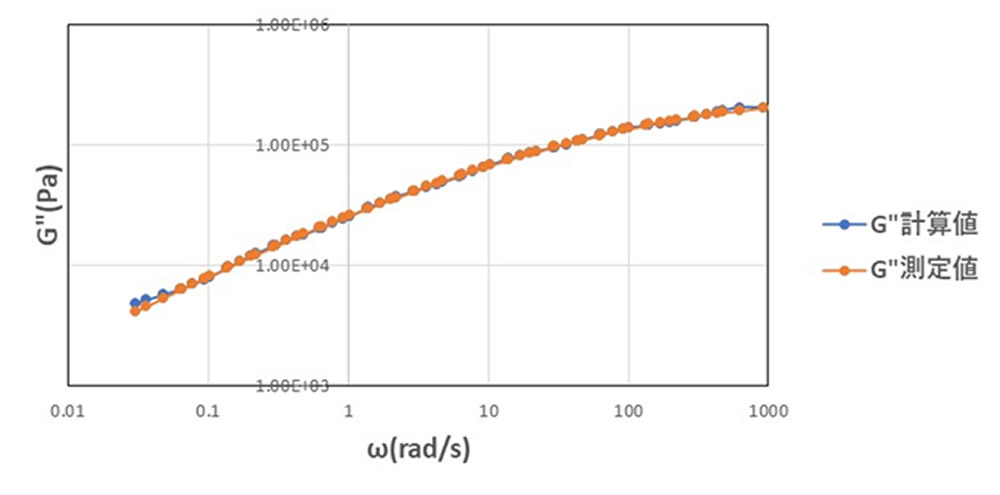
図3に最適値を用いたときの G’ の計算値と測定値の比較を示します。また、図4は G” の比較になります。どちらも計算値は測定値に重なっており、表1の値の精度は非常によいことがわかります。なお、列数 N を増やせば精度は向上していきますが、全体の特性にほとんど影響しないスペクトルも出てくるため、ある列数で飽和します。
参考URL:1)https://ja.helpr.me/9661-what-is-grg-nonlinear-solver
![]()
![]()
関連記事/関連ページ
●樹脂成形とレオロジー 第23回 「樹脂の周波数依存特性からわかること」
●樹脂成形とレオロジー 第25回「複素粘度の利用法」