樹脂成形とレオロジー第26回「円管内の流れの特性式と応用」
本講座の第9回において指数則流体の特性式の一部をご紹介しました。ここでは、円管流路内での特性式の詳細を記述するとともに、実成形での流動予測に役立つ形での検討を加えたいと思います。
1.円管内の流動式
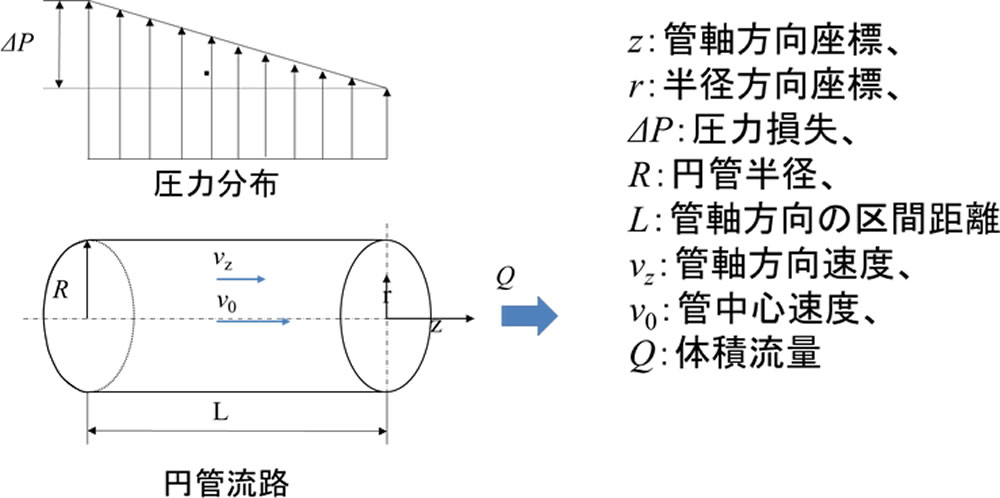
いま、同じ半径の一本の円管内を等温の非圧縮性流体が満たし、定常層流で流動し、管壁ですべりがなく、重力などの体積力が働かないと仮定します。円管流路諸元と流動時に生じる物理量の一部を図1に示します。この流路内でのニュートン流体の運動方程式の厳密解はハーゲンポアゼイユ流れ(Hagen-Poiseuille flow)として流体力学の教科書に必ず記載されています。指数則流体でも同様の手順で厳密解を求めることができます1)。
![]()
ニュートン流体と指数則流体での解の比較を表1に示します。ここで、κ:擬塑性粘度、 \(\dot{\gamma\ }\) :せん断速度、n:構造粘度指数です。流動方向が圧力勾配と逆になるため負号が付く式が出ますが、煩雑さを避けるために負号を取った形で取り扱うのが一般的です。なお、0 < n < 1が擬塑性流体、n =1がニュートン流体、1 < n がダイラタント流体とよばれます。プラスチックなどの高分子溶融体はほとんどが擬塑性流体としての特性を示します。
2.円管流路のランナーへの置き換え
樹脂成形では金型がよく用いられます。金型は溶融樹脂を注入するための通路が設けられており、製品を作るキャビティへ樹脂を導く通路がランナーとよばれています。ここでは円管流路をランナーとしたときの諸検討を行います。
2.1 樹脂物性値
![]()
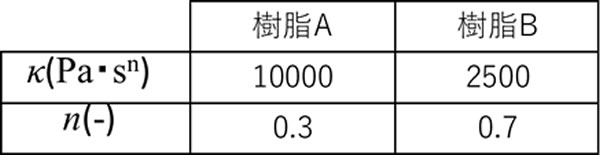
ここでは溶融状態の2種類の熱可塑性樹脂を模擬して表2に示す樹脂物性値を与えました。このとき粘度 \(\eta\) は表1にも示したように次式で計算できます。
\begin{align*}
\eta &= K \dot{\gamma} ^ {n-1} &\qquad ・・・・・・・(1)
\end{align*}
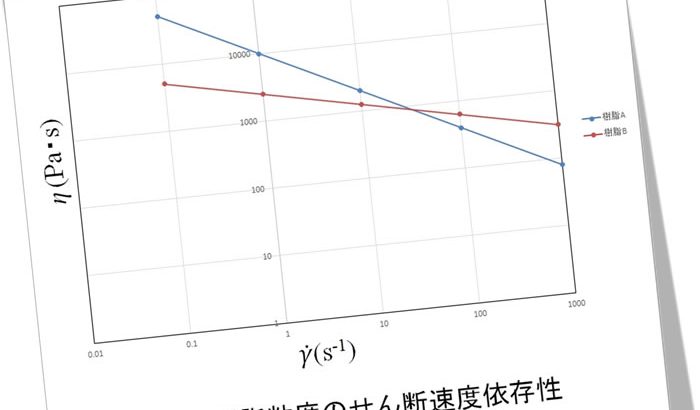
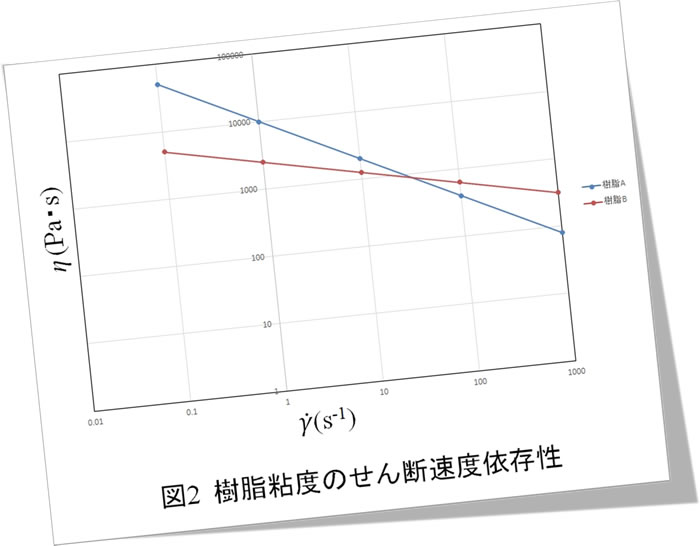
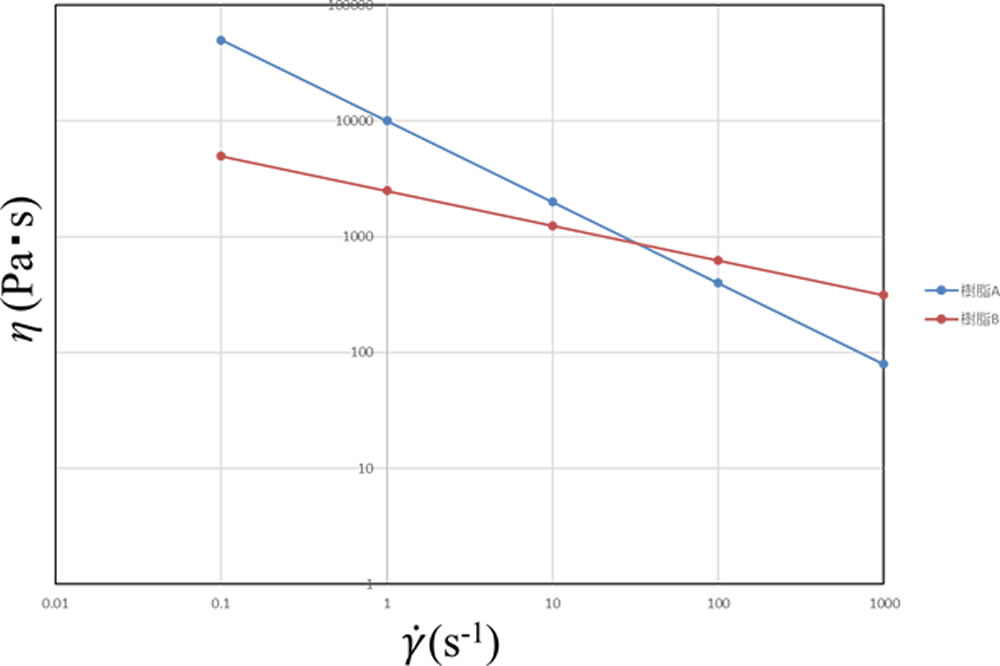
図2に樹脂粘度のせん断速度依存性を示します。横軸はせん断速度 \(\dot{\gamma\ }\) 、縦軸は粘度 \(\eta\) で、両対数座標上で表しています。樹脂Aと樹脂Bはせん断速度の増加とともに粘度が低下する擬塑性流体の特性を示しています。勾配が異なっており、 \(\dot{\gamma\ }\) が30s-1より小さいときは樹脂Aの粘度が高く、 \(\dot{\gamma\ }\) がそれより大きいときは樹脂Bの粘度が高くなっています。
![]()
2.2 流路諸元
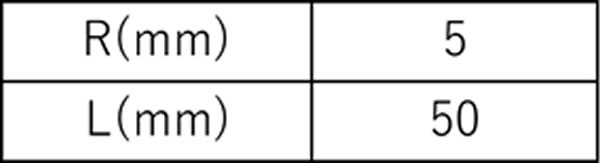
ここでは流路諸元を固定した検討を行いました。これを表3に示します。すなわち半径5mm、長さ50mmのランナーがあり、樹脂はここを通過してキャビティへ流入するとしておきます。
![]()
2.3 成形条件
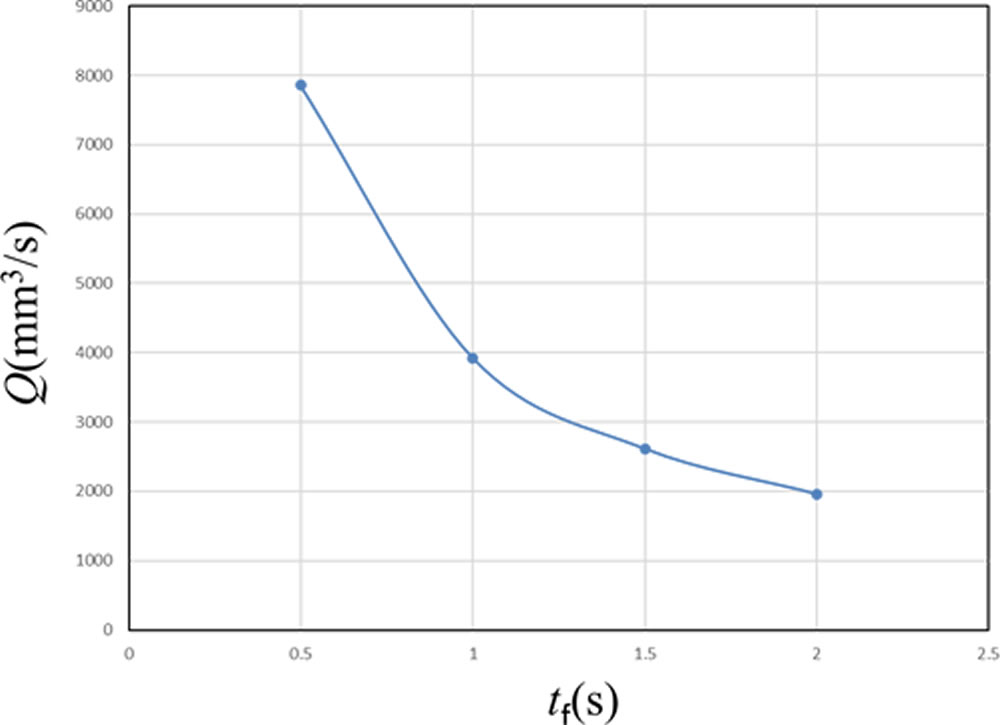
射出成形の場合、樹脂の注入時間は数秒で終わりますのでここでは0.5~2.0sの間をランナー部の通過時間 tf とし、このときの体積流量Q を次式で求めました。
\begin{align*}Q &= \frac{\pi R^2L}{t_f} &\qquad ・・・・・・・(11)\end{align*}
tf =0.5,1.0,1.5,2.0sを与えたときの tf とQ の関係を図3に示します。Q は2,000~8,000mm3/sの範囲にあります。
![]()
2.4 結果と考察
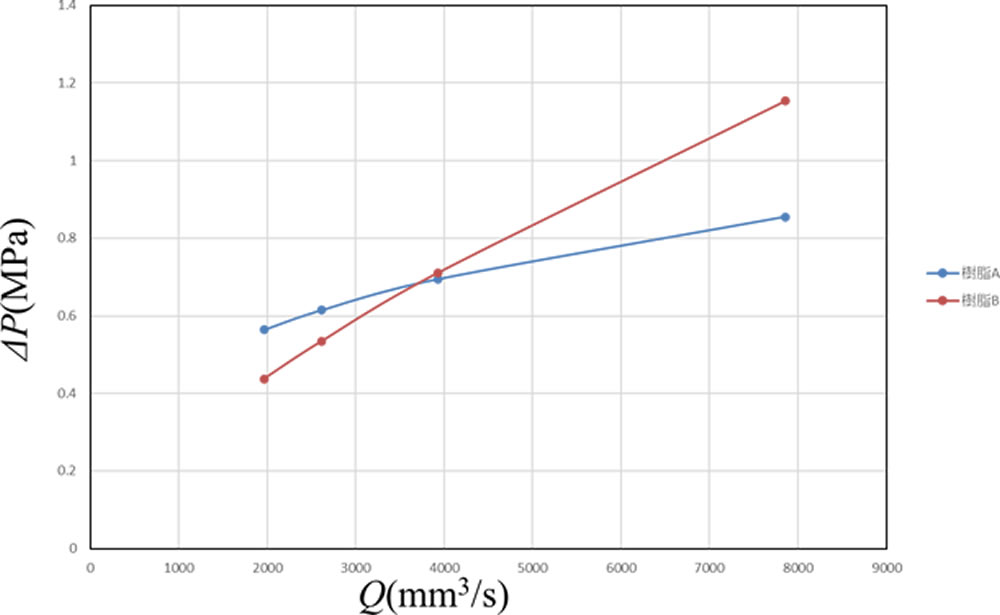
表1の(9-2)式を用いて圧力損失 \(\Delta\) P を計算しました。Q は図3に示した4点を使用しました。結果を図4に示します。どちらの樹脂もQ の増加とともに \(\Delta\) P も増加します。Q が少ないときには樹脂Aが樹脂Bよりも \(\Delta\) P が大きい、すなわち、同じ流量を流すのに上流側により大きな圧力を加える必要があることを示しています。Q の増加とともに両者の差が縮まり、4,000mm3/s手前( tf =1.0s)で同じ値となります。それより大きなQ では逆に樹脂Bの方がより大きな圧力を必要とします。次にこの理由について調べてみました。
![]()
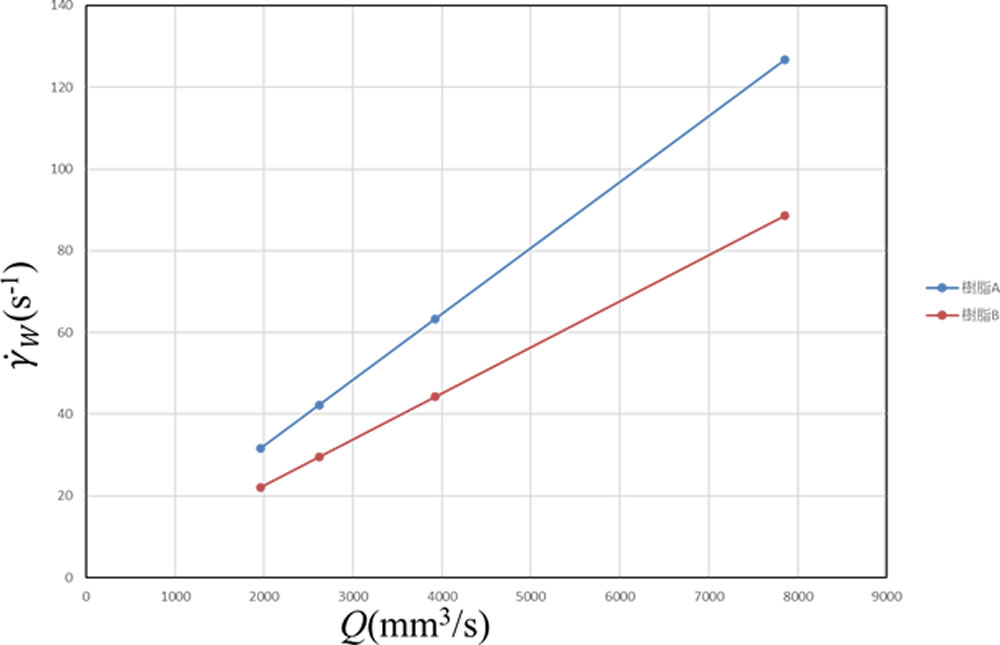
(4-2)式を用いてQ と管壁せん断速度 \(\dot{\gamma\ }\)w の関係が求められます。図5に結果を示します。どちらの樹脂も線形の特性になり、どのQ でも樹脂Aの方が樹脂Bよりも大きなせん断速度になっています。
![]()
次に(1)式を管壁の位置に適用すると次式が得られます。
\begin{align*}
\eta_{w} &= K \dot{\gamma} w ^ {n-1} &\qquad ・・・・・・・(12)
\end{align*}
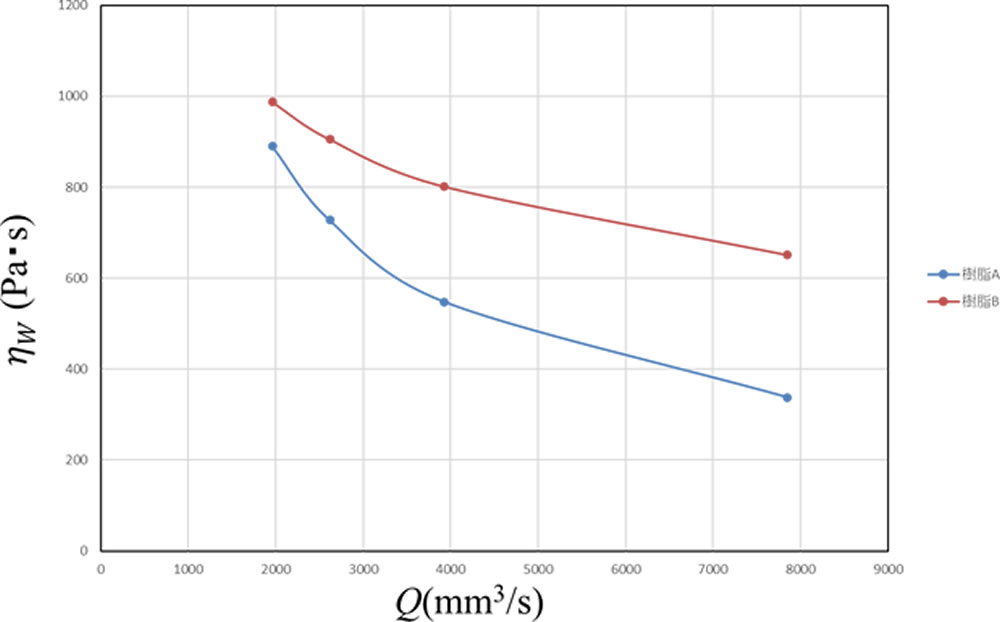
ここで \(\eta\) w:管壁における粘度です。 (12)式を用いて \(\eta\) wを求め、Q と \(\eta\) wの関係を調べました。結果を図6に示します。どのQ でも樹脂Bの方が樹脂Aよりも大きな粘度になっています。
![]()
表1では管壁せん断応力 \(\tau\) wは(2)式の形になっていますが、次式でも求められます。ここではこれを使います。
\begin{align*}
\tau_{w} &= \eta_w \dot{\gamma}_w &\qquad ・・・・・・・(13)
\end{align*}
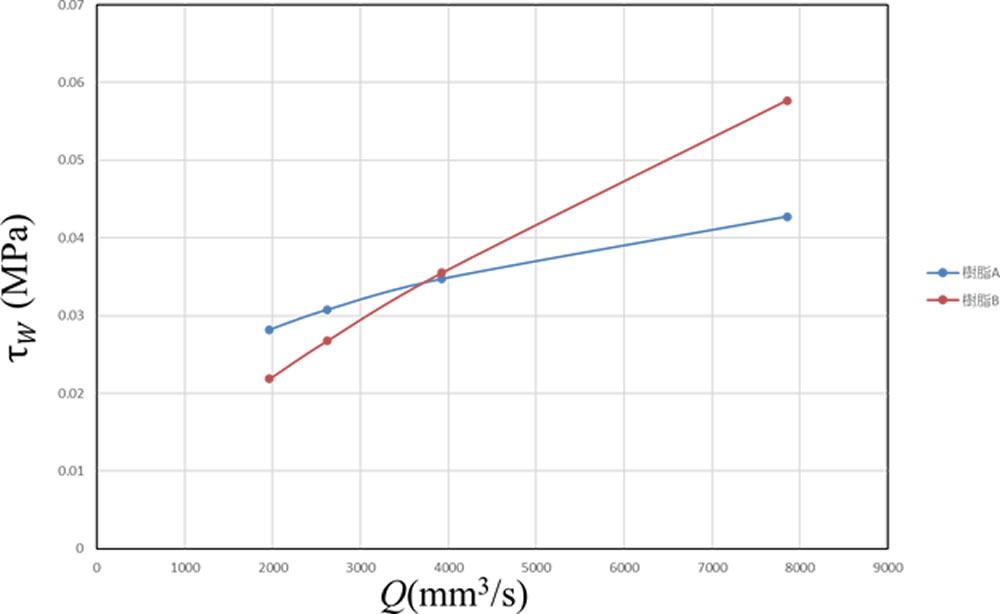
Q と \(\tau\) wの関係を図7に示します。ここで図7と図4は同じ形をしています。(2)式のように \(\tau\) wと \(\Delta\) P は比例関係にありますのでそのようになります。 \(\eta\) wと \(\dot{\gamma\ }\)wの積が図4のような特性を生み出しています。
![]()
なお、(9-2)式では分母にR 、分子にL という流路諸元が入りますので、これらの値によっても \(\Delta\) P が大きく変わってきます。このように金型内の流動挙動は樹脂物性値、成形条件、流路諸元が絡んで複雑に変化しますので、表1に示した式をうまく利用して流動予測に役立てることが有効です。
参考文献:1)J. M. McKelvey, “Polymer Processing,” John Wiley and Sons, New York, 1962.
関連記事/関連ページ