樹脂成形とレオロジー第36回「気液二相流体の見かけ粘度（体積流量率粘度）」
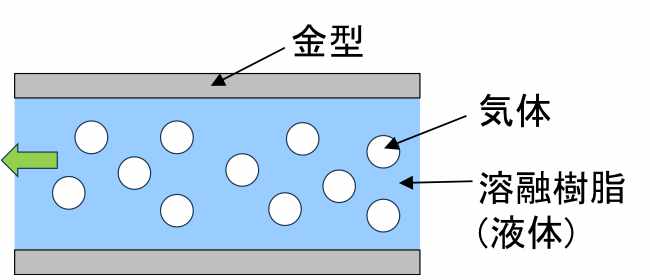
樹脂成形品は断熱性、遮音性の確保や軽量化のために気泡を含むタイプのものが存在します。発泡のさせ方は樹脂にブレンドした発泡剤を減圧、加熱、化学反応などにより気化させる方法を用います。成形中は図1のように溶融樹脂と気体の二相流となって金型内を流動します。この流れは、機械工学便覧の定義によると「気体と液体が混ざった混相流で、両者の流量の割合で種々の流れのパターンが観察される。固液二相流や固気二相流に比べての特徴は気相と液相の界面が変化することである。さらに粒子状態となった気泡や液滴が分裂と合体を繰り返すため、微視的観点に立つと現象は極めて複雑である。」と記載されています。このため、特にプラント設計の分野では気体と液体の接触の仕方で分類し、それぞれで圧力損失の予測式を立てる方式を用いています。このように厳密にはかなり複雑な現象ですが、見かけ粘度を簡便に見積もる方法も提案されており、ここではその中で使いやすい「体積流量率粘度」について説明します。
体積流量率粘度とは
気体と液体が混じった二相流の見かけ粘度は、基本的には気体と液体の粘度ならびに気体の占める体積割合で定義できます。この例を(1)式に示します1)。ここで、\(\eta\)m：気液二相流体見かけ粘度、\(\eta\)g：気体粘度、\(\eta\)L：液体粘度、 \(\beta\) ：気体体積流量率です。
\begin{align*}
\eta_m = \beta \eta_g + (1 – \beta) \eta_L
\hfill \qquad\text{・・・・・・・(1)}
\end{align*}
AL-Sheikhらは(1)式を気液二相流における流動様式の判定に使う次元解析式に適用しました2)。また、Kasturiらは気液二相流の気液間に滑りがない場合の圧力損失を算定するために(1)式の見かけ粘度を用いました3)。
また、\(\beta\)は次式で示されます。
\begin{align*}
\beta = \frac{Q_g}{Q_g + Q_L}
\hfill \qquad\text{・・・・・・・(2)}
\end{align*}
Qg：気体体積流量、QL：液体体積流量
ここで次のように比粘度\(\eta\)rを定義します。
\begin{align*}
\eta_r = \frac{\eta_m}{\eta_L}
\hfill \qquad\text{・・・・・・・(3)}
\end{align*}
これから(1)式は次式となります。
\begin{align*}
\eta_r = 1 – \beta \left( 1 – \frac{\eta_g}{\eta_L} \right)
\hfill \qquad\text{・・・・・・・(4)}
\end{align*}
溶融樹脂中に気体が存在する場合、\(\eta\)g \(\ll\) \(\eta\)Lなので(4)式は次式となります。
\begin{align*}
\eta_r = 1 – \beta
\hfill \qquad\text{・・・・・・・(5)}
\end{align*}
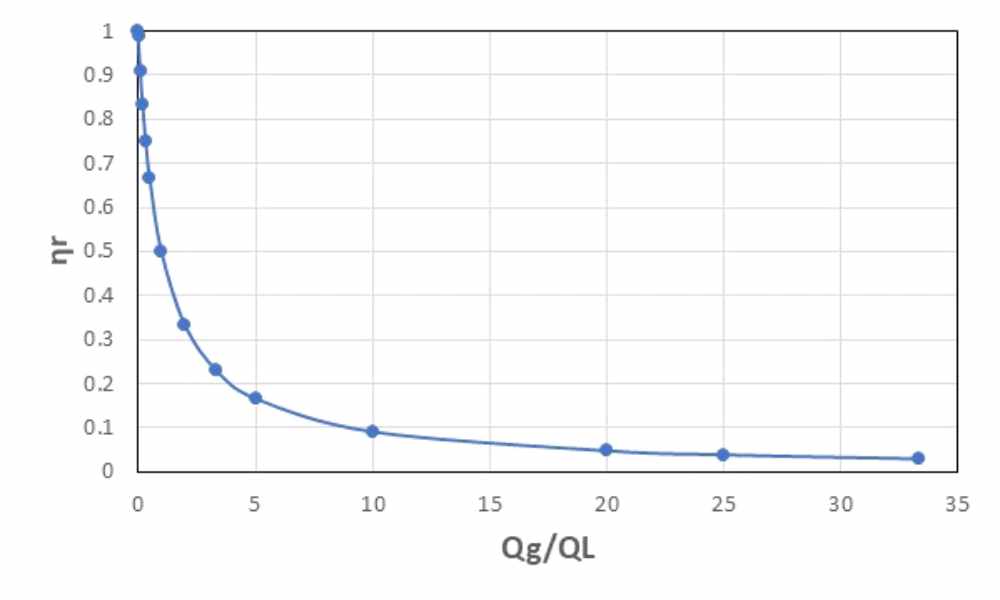
Qg / QLと\(\eta\)rの関係を図2に示します。気体側の体積流量比率が増えるにしたがって比粘度\(\eta\)rは低下していきます。気体とその周りの液体が同速度で同方向に移動する場合、体積流量比率は体積比率とみなすことができます。図2の関係を用いて気液二相流が流動中の圧力損失などの予測に役立てることができます。
なお、この他に「重量流量率粘度」、「Einstein型粘度」、「相当液体粘度係数」等の表し方1)もあります。
参考文献
1)松村博久：気液二相流体の粘性係数についての一考察, 鹿児島大学工学部研究報告, 21,55-61,1979-09.
2)AL-Sheikh, J.N, .Sannders, D.E. and Brodkey, B.S.: Canadian J. Chem. Eng., 48,(1970),21.
3)Kasturi,G. and Stepanek, J.B,: Two-Phase Flow-I. Pressure drop and void fraction measurements in cocurrent gas-liquid flow in a coil, Chem. Eng. Sci., 37(1972),1871.
関連記事/関連ページ