Benchmark Problems for Simulating
Electric Fields Near Sharp Corners
（鋭角付近の電場をシミュレートするベンチマーク問題）

Doug Craigen, PhD
Integrated Engineering Software/Enginia Research
Winnipeg, Manitoba, Canada R3H 0G4

見出し

 

問題

Jacksonの解

ケース 1: 鋭い角

ケース 2: 90度の角

まとめ

問題

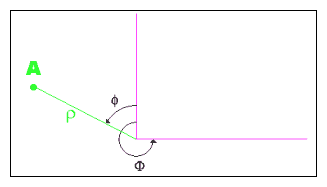電磁場シミュレーションでよくある質問のひとつは、”最大値はいくつでどこになるか？”ということです。ある種のコーナー又はエッジがあるとき、その質問は扱いにくいものとなります。コーナーは数学的に特異です。それに近づく方向に依存する、コーナーでフィールドの方向について、質問することはできません。さらに左のようなケースでは、そのフィールドの大きさはコーナーで無限大になるため、コーナー近くのフィールドを調べると、だんだん大きくなるフィールドが得られます。その質問は、コーナーにどのように近づくかに依存するので、意味がありません。

もちろん、どの物理的なオブジェクトも完全なコーナーを持たない、すなわちいくらかの丸みがあります。また、フィールドが極めて高くなる位置で、他の現象が働きそのフィールドを制限します。それで、そのフィールドが最大値を持つ、その値についての理由は自明ではありません。電磁界CAEツールのユーザーは、解が物理的に正しく見えることに安心し、しばしば安全という意味で間違う ことがあります。しかしながら、そのコーナーを鋭角に描くとすると、作成したモデルの正しい解は、そのコーナーでフィールドは特異になることです。CAEツールがこれを予測しなければ、質問に対する間違った解を与えています。これはその実際問題に対する正しい解であるかもないかも知れないが、もしそれが正しければ、その正しい物理的問題を解くことができるというよりも、むしろ運が良かったのです。そのソルバーにもっと高精度の収束値をセットしたり、又はコーナーまわりのメッシュを細かくすると、もっと大きな”最大フィールド”を得るでしょう。これはシミュレーションに対するロシアンルーレットのアプローチになります。

ツールが提起された疑問に対する正しい解を与えるとするための正しいアプローチについて、いつも議論してきました。ユーザーに、幸運に頼らずに知的な方法で使えるツールを提供するためのキーとなるのは、現実的に実際の物理的な問題を反映する質問を提起することです。従って、第1レベルのベンチマークは、測定が不確実で、テストケースのモデル化が争点でないようなケースです。

Jacksonの解

J.D. Jackson著「Classical Electrodynamics, 2^nd Edition」では、2.11節の上部に解説された一般的な問題を扱っています。
コーナーの十分近くで、その電位は次の式になることを示している：

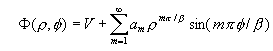
この式を使用して、解析的に定義されたコーナー問題を持ち、その中でa_mを決めるという問題を作ることができます。
例題を図２に示す：

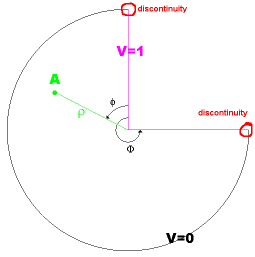図２：解析的に解ける問題

 

この問題ではもちろん、1 Vと0 Vの区切りが接することはできません。しかしながら、それらが限りなく近づくという取り扱いをすれば、数学的には何の問題もありません。作成される任意のモデルで、小さな不連続がこれらの位置で必要となります。

その円弧の半径を1 mとし、円弧上の任意位置Pを考える：

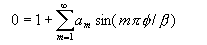
これは既知の解を持つフーリエ級数問題である：

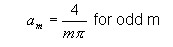
それで、そのフィールド成分は：

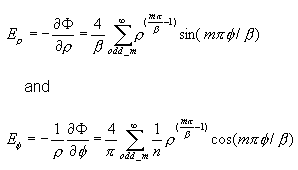
ケース #1: "鋭い角" ()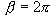

これは非常に鋭い角、薄膜などの、最も極端なケースである。 選ばれたモデルを図３に示す：

図３：レーザーエッジモデル

 

モデルは0 Vに設定された半径1 mの円と、1 Vにセットされた(0,0)から(-0.99,0)までのラインセグメントからなります。 このモデルを、2D電界シミュレーションパッケージELECTROで解析します。

バージョン6.1以前のElectroユーザーは"境界要素法" (BEM) ソルバーを持つだけでした。ほとんどの電界シミュレーション問題には、依然としてこれを使用することを勧めます。FEMソルバーの品質について、悪い印象を与えることを避けて説明するために、ELECTROと、長年"有限要素法" (FEM)を使用している競合製品のひとつと比較しました。

その結果を簡単に解説すると、標準的な標本点列は、正のx軸に沿って与えられています。ここで、Eのy成分は ゼロになります。

クイックテストとして、その値をx=0.01で調べます。それはコーナーから形状サイズの1 %の距離での フィールドを求めることを意味します。明らかに、ELECTROのソルバーは時間が長くなるほど解はよくなります。

 

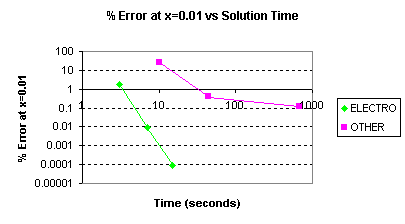図４：BEM (Electro) と FEM (Other) 精度と解析時間の比較

 

"境界要素法"を使うことで、ELECTROはより良い解を早く求めることができます。
その理由は、それぞれの方法で計算に使用したメッシュを調べてみれば、明らかです：

 

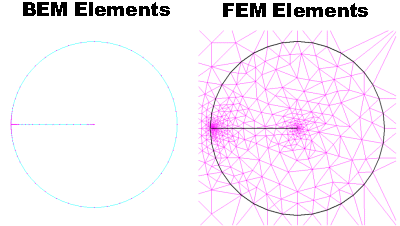図５：BEM と FEM 要素の比較

 

BEM要素はこの問題では純粋なサーフェス要素になり、与えられた電位になるように、電荷分布をモデル化するために使用されます。FEM要素は局所的な電位を計算するために使用する面積（エリア）です。 BEMでもっと小さい細部を含むメッシュを作り易いだけでなく、電界は電荷から積分によって計算され、電位を微分するよりも数値的な誤差が少なくなります。

次の３つの表では、２つの方法の違いをさらに詳細に調べている：

 

デフォルト設定の解 (Electro: 3 seconds, Other: 10 seconds) % error in ( )'s
x	解析解 E	ELECTRO	OTHER	注意： ・ELECTRO (BEM) は３倍早い ・ELECTRO はいずれのケースでももっと精確な数値を与える ・x=0.8というチャレンジではない位置でも、ELECTRO は7倍以上精度 　が良い 長年に渡る数値的なソルバーの比較を元にして、この問題におけるBEMと比較した任意のFEMコードに対して、我々はこれと同じ一般的な傾向が見られることを予想している。
0.8	0.395423635	0.39512 (0.078%)	0.3975 (0.53%)
0.1	1.83015317	1.8262 (0.22%)	1.861 (1.7%)
0.01	6.303166063	6.185 (1.9%)	8.048 (28%)
0.001	20.11157327	16.94 (16%)	12.66 (37%)
0.0001	63.65561168	33.55 (47%)	12.94 (80%)
0.00001	201.3148353	94.09 (53%)	12.96 (94%)
0.000001	636.6191357	94.09 (85%)	12.97 (98%)

 

どちらのプログラムも容易にもっと精度良く解くようにセットでき、これはデフォルト設定を使用し得られるものでした。
下の表は、各プログラムで高精度の設定で得られる解である：

 

修正したソルバー設定 (Electro: 7 seconds, Other: 44 seconds) % error in ( )'s
x	解析解 E	ELECTRO	OTHER	注意： ・両方のプログラムはより良い解を与えている ・ELECTROの解は、"他の"解に比べて６倍早い ・ELECTROは形状スケールの 1/10,000に対して、1 %の精度向上を示している
0.8	0.395423635	0.3954183 (0.0014%)	0.39557 (0.037%)
0.1	1.83015317	1.830127 (0.0014%)	1.83046 (0.017%)
0.01	6.303166063	6.302590 (0.0091%)	6.32766 (0.39%)
0.001	20.11157327	20.09547 (0.080%)	20.372 (1.3%)
0.0001	63.65561168	63.13316 (0.82%)	82.51 (30%)
0.00001	201.3148353	184.0527 (8.6%)	101.66 (50%)
0.000001	636.6191357	405.6363 (36%)	102.97 (84%)

 

修正したソルバー設定 (Electro: 15 seconds, Other: 686 seconds) % error in ( )'s
x	解析解 E	ELECTRO	OTHER	注意： ELECTROは再びすべての位置で大きく改善している "Other"は0.8, 0.1および0.01で大きく改善しているだけである ELECTROでは15 秒で、その解は形状スケールサイズの百万分の一に対して、2-3%の精度にまで到達できる
0.8	0.395423635	0.3954213 (0.00059%)	3.95455 (0.0079%)
0.1	1.83015317	1.830155 (0.00010%)	1.83144 (0.070%)
0.01	6.303166063	6.303172 (0.000094%)	6.29532 (0.12%)
0.001	20.11157327	20.11122 (0.0018%)	19.6486 (2.3%)
0.0001	63.65561168	63.64274 (0.020%)	55.6532 (12.6%)
0.00001	201.3148353	200.88 (0.22%)	106.412 (47%)
0.000001	636.6191357	621.25 (2.4%)	108.311 (83%)

 

両方の方法で、興味のある領域でより良い解を得るために、局所的にメッシュを細かくするようにできます。

ケース #2: 90度の角 ()

図６は90^oのコーナーを持つ提案したベンチマーク問題を示しています。これはケース #1よりもっと多い典型的な問題タイプです。その特異性は重大ではないが、1 Vのパイ片と0 Vの円の間のギャップによって、その問題を困難なものにしています。これはコーナーを持つことでより実世界の問題であるが、他の形状もまた解に影響します。事実、ギャップ中のEフィールドの既知の解に対して、これをまたベンチマークとして使用できます。小さなギャップに対して、これはまた困難な問題となります。

 

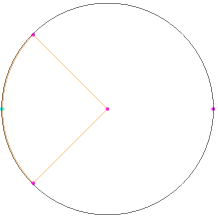図６： 90o コーナー問題

 

下の表は結果のまとめです。今度は"長い"計算に焦点を当てています （ここで、"長い"という言葉は、どのソルバータイプが使用されたかを比較して、理解するべきです）。

 

修正したソルバー設定 (Electro: 20 seconds, Other: 323 seconds) % error in ( )'s
x	解析解 E	ELECTRO	OTHER
0.8	0.52469989	0.524710 (0.0019%)	0.524786 (0.01%)
0.1	1.747623467	1.747621 (0.00014%)	1.7504 (0.15%)
0.01	3.931432953	3.931284 (0.0038%)	3.93625 (0.12%)
0.001	8.4874	8.4854 (0.023%)	8.567 (0.93%)
0.0001	18.287	18.202 (0.46%)	18.61 (1.8%)
0.00001	39.40	35.80 (9.1%)	19.74 (50%)
0.000001	84.88	57.10 (32.7%)	19.82 (77%)

 

BEMは再び優れたスピードと精度を示しています。これはELECTRO内の新しいFEMコードを使ってダブルチェックをすることができます。

 

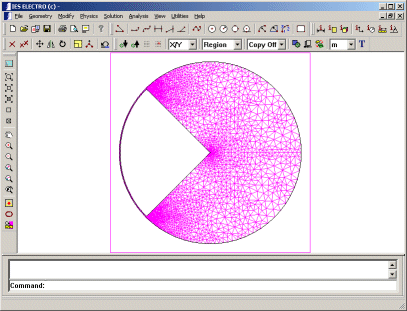図７： ELECTRO FEM 要素

 

x	解析解 E	ELECTRO FEM Solution 90 seconds	注意： ・ELECTRO FEM 解は、"Other" FEMプログラムが323秒に対して90秒であり、その誤差はいくつかの位置で大きく、その他の位置では小さい ・このタイプの問題に対するFEM対BEMの全体的な結論は変わらない
0.8	0.52469989	0.5229 (0.34%)
0.1	1.747623467	1.74528 (0.13%)
0.01	3.931432953	3.821 (2.8%)
0.001	8.4874	8.4891 (0.02%)
0.0001	18.287	18.567 (1.5%)
0.00001	39.40	34.89 (11%)
0.000001	84.88	39.47 (53%)

まとめ

設定は簡単でも解くのが困難な問題タイプを、モデル中のコーナー又は鋭いエッジの付近で、精確なフィールド値を与えることで、CAEシミュレーションソフトウェアの能力をベンチマークするために、提案しています。このタイプのふたつのケースで、何故我々が境界要素法がこの問題に対して好ましいソルバータイプであると信じているか、ということを示しています。

 

他のプログラムを持つユーザが、比較のために計算をおこなうのと、その相対的なスピードと精度を検証するために、30日間の無償の評価使用をするようにお勧めします。

 

この研究で"Other"プログラムのユーザは、フィールドが放電やフラッシュオーバーが起こるほど十分高いとき、小さなフィーチャーまわりの解が適切な予測をするには、十分な精度ではないことを考察する良い理由になります。

この研究に使用した計算機は2.4 GHzで、Windows 2000を使用しています。

※開発元：Integrated Engineering Software