樹脂成形とレオロジー 第15回「 減衰反応速度式」
前回、熱硬化性樹脂の反応速度は温度と反応率の関数になることを述べました。今回は化学分野でよく用いられる減衰反応速度式について説明します。
1. 温度依存性を表すモデル
同じ材料であっても温度が高いと反応は活発になり、温度が低いと反応はゆるやかに進みます。反応速度の温度依存性を表すもっとも一般的な方法は、アレニウスモデルを用いることです。アレニウスモデルは、ある温度での化学反応を予測する式としてスウェーデンの化学者アレニウスが提案したもので、現在では反応の温度依存性を表す標準的な手法として広く活用されています。アレニウスの式は次の形になります。
![]()
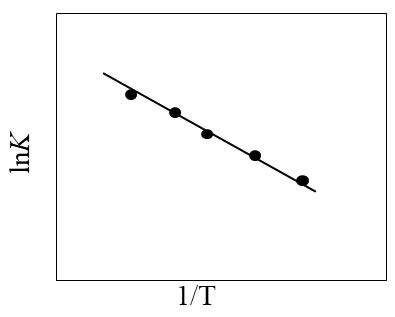
ここで、K:反応速度定数、Ka :頻度因子(温度に無関係な定数)、 E :活性化エネルギー(アレニウスパラメータともいう)、R:ガス定数、T:絶対温度です。Kaが同じなら、Tが高いほど、Eが小さいほどKは大きくなります。横軸を1/T、縦軸をlnKとした片対数座標上で図1のような一定勾配の負の直線関係が得られれば、その現象はアレニウスの式に従っているといえます。
![]()
また、CAEではRは表示する必要がないので次式のように定数を置き換えます。
![]()
そうすると(1)式は次の形になります。
![]()
![]()
2. 温度、反応率依存モデル
2.1 モデル式と基本特性
一般的な化学反応では、反応物の消費と生成物の産出がもっとも活発に行われるのは、相手剤と結合する頻度が高い初期時刻になります。この場合は等温状態で初期に反応速度が最大になり、次第に減衰していくモデルが適合します。これは温度依存性もまとめて次の形になります。
![]()
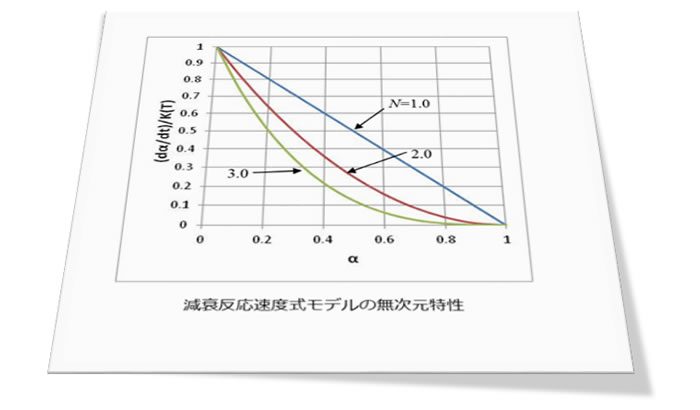
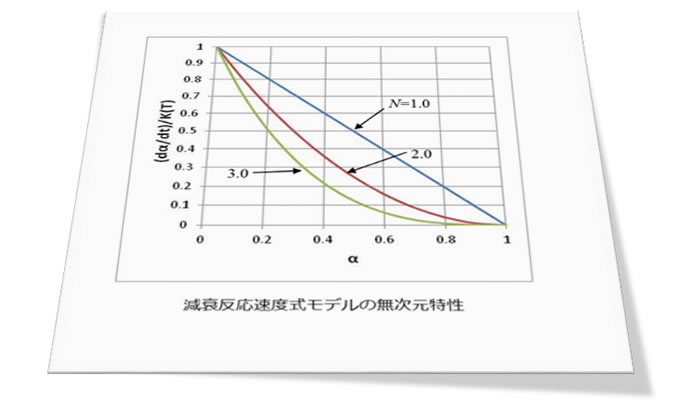
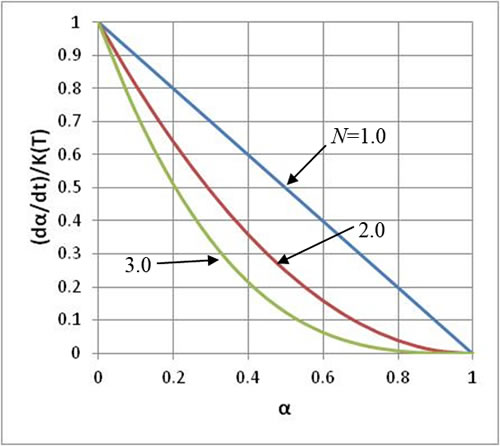
ここでα:反応率、dα/dt:反応速度、K(T):温度依存係数、N:樹脂固有の係数です。(4)式をK(T)で除した無次元反応速度特性を図2に示します。反応の進行(αの増加)とともに無次元反応速度は減衰していきます。Nが大きくなるにしたがって早く減衰します。化学の分野ではNの値を用いて1次反応、2次反応などとよびます。なお、CAEではNはフィッティングパラメータの一つなので、正の実数を割り当てます。
![]()
2.2 反応速度、反応率の変化
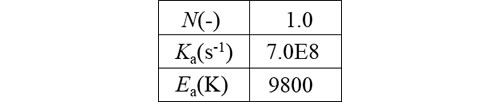
ここでは表1のように係数を固定して特性を調べてみます。
![]()
2.2.1 等温特性例
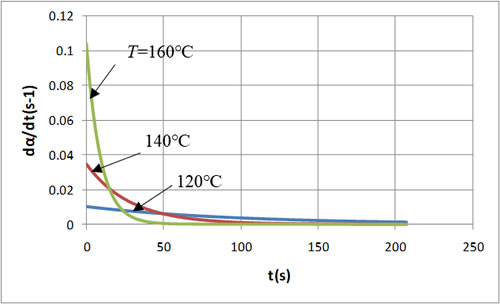
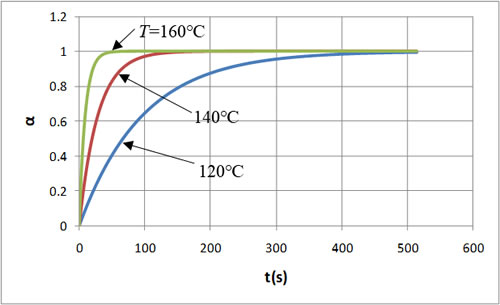
まず、温度をパラメータとし、それぞれの温度に保った場合の特性を比較します。図3は反応速度の時間変化で、温度が高いほど反応速度の初期値は大きくなり、時間の経過とともに急速に減衰していくことがわかります。温度が低いと反応速度の初期値は小さいが、時間をかけて減衰していく特性となります。図4は反応率の時間変化で、温度が高いほど反応が急激に進み、短い時間で反応が終了していることがわかります。
![]()
![]()
2.2.2 昇温特性例
次に昇温速度をパラメータとした場合の特性を比較します。
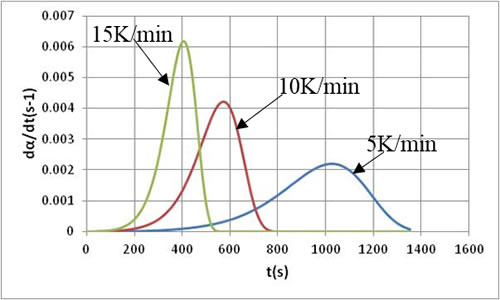
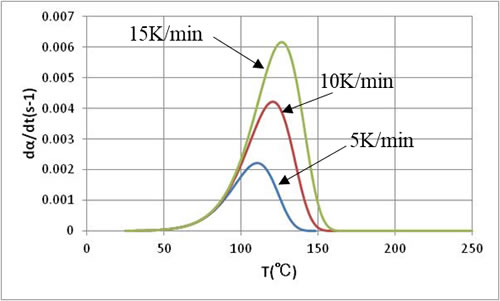
図5は反応速度の時間変化で、等温特性とは異なり、反応時間の途中に最大値が存在します。これは温度上昇による反応の活性化と時間の経過による反応の減衰が同時に起きた結果です。昇温速度が速いほど最大値は大きくなり、短時間に減衰します。
![]()
図6は反応率の時間変化で、昇温速度が速いほど短時間に反応が進行することがわかります。
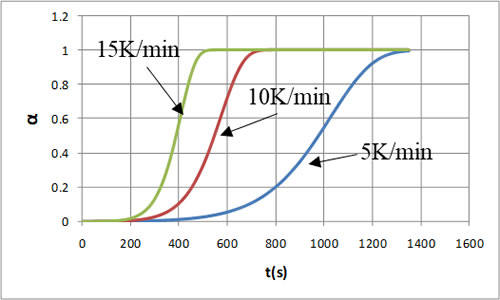
![]()
横軸を温度にした場合の特性を図7、図8に示します。このようにすると横軸の広がりが抑えられ図が見やすくなるので、昇温特性の場合は通常温度を横軸にします。このようにすると昇温速度が遅いほど低い温度で反応が終了しています。
![]()
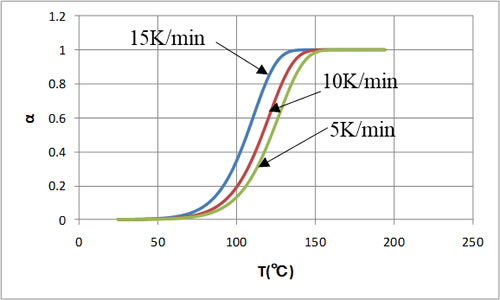
![]()
次回は等温状態でも発熱速度のピーク時刻を変えられるモデル式について説明します。
関連記事/関連ページ
●樹脂成形とレオロジー 第14回 「熱硬化性樹脂の反応の進行」
●樹脂成形とレオロジー 第16回 「Kamalの反応速度モデル」