溶融樹脂の粘度はせん断速度に依存します。このため、色々なモデル式が提案されてきました。本講座でもそれらの詳細を説明してきました。ここでは、各種モデル式を用い、その特性曲線を並べてみることにしました。これにより、粘度測定実験結果がどのモデルに合致するかという判断の一助になれば幸いです。
表1にせん断速度依存粘度式モデルを示します。指数(べき乗)則(Power law)モデルは高分子溶融体用に古くから用いられてきました。Crossモデルは現在よく使われています。 Modified CrossモデルはCrossモデルの改良形です。CarreauモデルもCrossモデルの代わりに使われ、その拡張型としてCarreau-Yasudaモデルがあります。ビンガム塑性流体モデル、Herschel-Bulkleyモデル、Modified Herschel-Bulkleyモデルはいずれも降伏値を持つ流体用です。
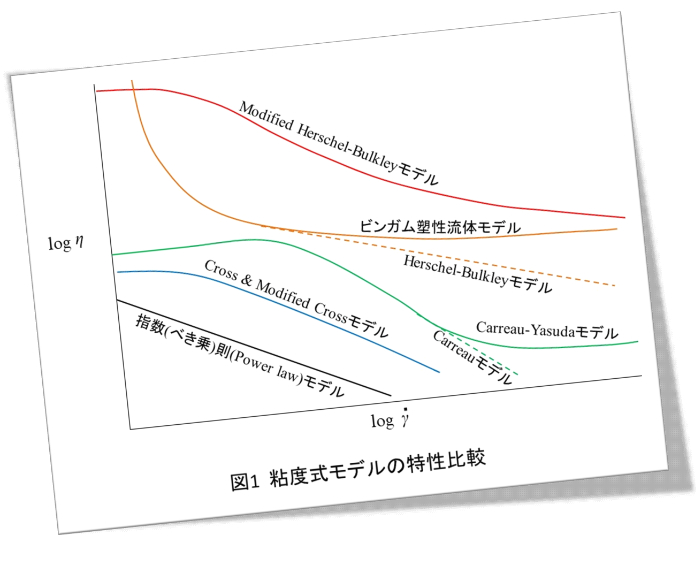
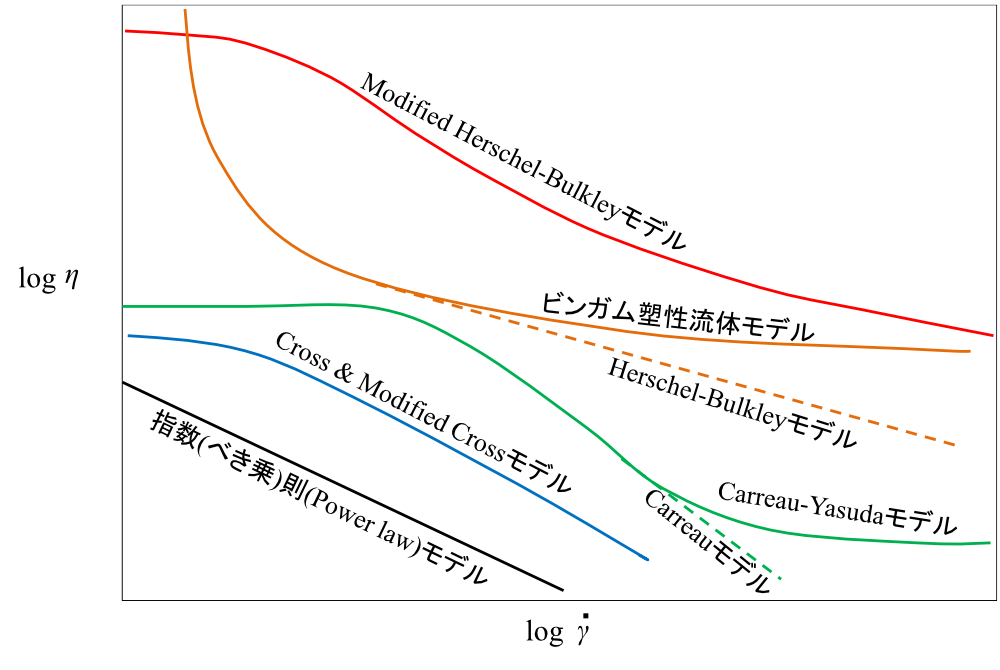
図1に粘度式モデルの特性比較を示します。縦軸は粘度、横軸はせん断速度で両対数表示にしてあります。この座標軸上で直線関係が得られたら指数(べき乗)則(Power law)モデルが合致します。せん断速度が小さくなると一定粘度に飽和し、せん断速度が大きくなると粘度が低下する特性ではCross 、Modified CrossモデルあるいはCarreauモデルが合致します。せん断速度がかなり大きくなると飽和粘度に近づく場合はCarreau-Yasudaモデルが合致します。せん断速度が小さくなると急激に粘度が上昇する場合は、降伏値を持つ流体の特性になり、ビンガム塑性流体モデルかHerschel-Bulkleyモデルが合致します。せん断速度の増加とともに粘度が飽和値に漸近する場合はビンガム塑性流体モデルになり、粘度が低下を続ける場合はHerschel-Bulkleyモデルになります。Modified Herschel-Bulkleyモデルはせん断速度が小さくなると飽和値になる特性を持たせており、せん断速度が非常に小さいときに粘度の値の発散を防ぐ機能を持たせてあります。
なお、各種モデルの係数の最適化手法につきましては弊社「樹脂流動解析スキルアップセミナー」で実習できます。
関連記事/関連ページ
●樹脂成形とレオロジー第34回「降伏値を持つ擬塑性流体」
●樹脂成形とレオロジー第36回「気液二相流体の見かけ粘度（体積流量率粘度）」
