概要
モータ設計において、「トルク効率の向上」「トルクリップルの低減」「低コスト化」などが目標の１つとしてあげられます。トレードオフの関係にある複数の目標を可能な限り同時に満たすモータの形状を求めるためにJMAGの形状最適化機能を利用します。
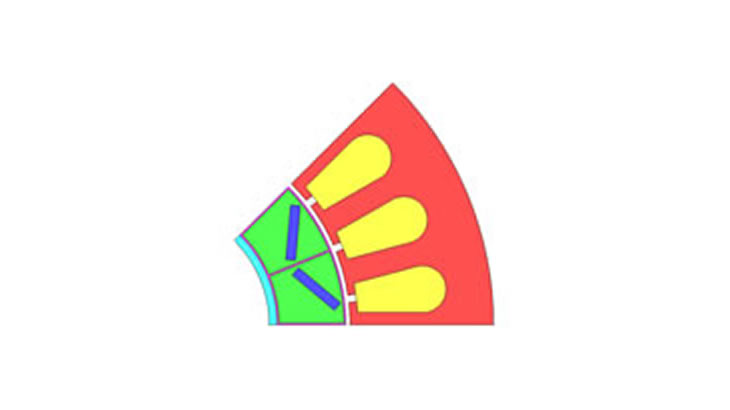
IPM構造モータのモデル
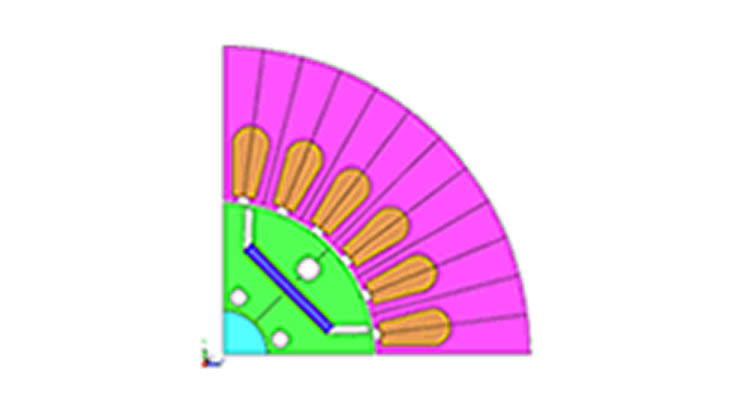
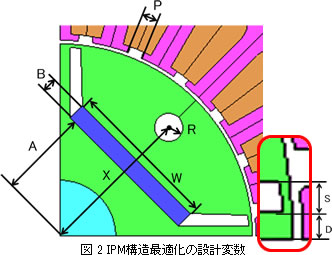
以下の1/4対称（反周期境界）の断面形状でモデル化し「シャフト、永久磁石、ロータコア」にかかるトルクを計算します。
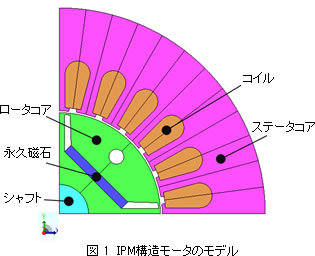
設計変数と制約条件の設定
「永久磁石の厚さ B」、「永久磁石の幅 W」、「空気領域の位置 X」、 「空気領域の半径 R」、「フラックスバリアの幅 S」、「フラックスバリアと1/4対称境界の垂直距離 D」を設計変数とします。部品同士が干渉しないように制約条件を設定します。
目的関数と最適化エンジンの設定
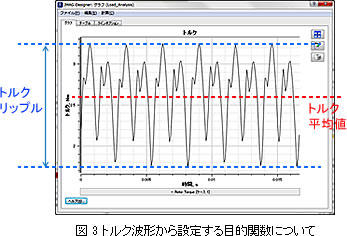
- 「トルク平均値の最大化」を目的関数とします
- 「トルクリップルの最小化」を目的関数とします
- 「永久磁石の体積の最小化」を目的関数とします
- 多目的最適化に適している「多目的遺伝的アルゴリズム」を最適化エンジンとして選択します
目的関数と最適化エンジンの設定
- 「トルク平均値の最大化」を目的関数とします
- 「トルクリップルの最小化」を目的関数とします
- 「永久磁石の体積の最小化」を目的関数とします
- 多目的最適化に適している「多目的遺伝的アルゴリズム」を最適化エンジンとして選択します
● 形状最適化結果
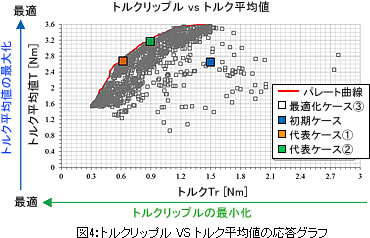
トルクリップル VS トルク平均値の応答グラフ
「トルクリップル」VS「トルク平均値」の応答グラフを図4に示します。 「トルクリップル」が小さく、「トルク平均値」が大きい解ほど最適化されています。目的関数「トルクリップルの最小化」と目的関数「トルク平均値の最大化」がトレードオフの関係にあるため、パレート曲線（トレードオフカーブ）を求めることが出来ます。※パレート曲線は、最適解の集合です。
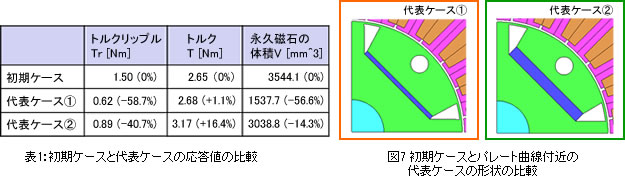
解の集合から代表してパレート曲線付近の解を2つ図4に示します。
代表ケース①：
トルクリップルの最小化を重視した解
代表ケース②：
トルク平均値の最大化を重視した解
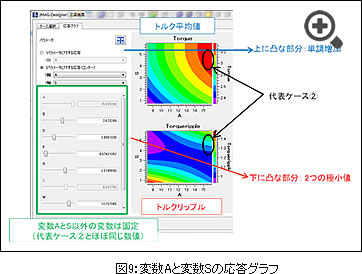
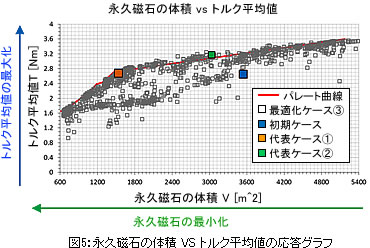
永久磁石の体積VSトルク平均値の応答グラフ
「永久磁石の体積」VS「トルク平均値」の応答グラフを図5に示します。
代表ケース①、代表ケース②の解を図5に示します。
「永久磁石の体積」が小さく、「トルク平均値」が大きい解ほど最適化されています。目的関数「永久磁石の体積の最小化」と目的関数「トルク平均値の最大化」がトレードオフの関係にあるため、パレート曲線（トレードオフカーブ）を求めることが出来ます。
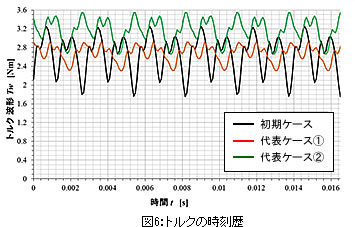
初期ケースと代表ケースのトルク波形
初期ケース、代表ケース①、代表ケース②のトルク波形を図6に示します。
初期ケースと代表ケースの形状と応答値の比較
「永久磁石の体積」VS「トルク平均値」の応答グラフを図5に示します。
代表ケース①、代表ケース②の解を図5に示します。
「永久磁石の体積」が小さく、「トルク平均値」が大きい解ほど最適化されています。目的関数「永久磁石の体積の最小化」と目的関数「トルク平均値の最大化」がトレードオフの関係にあるため、パレート曲線（トレードオフカーブ）を求めることが出来ます。
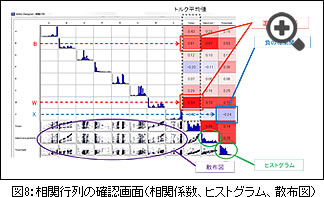
相関係数
図8の相関行列右上の−1以上1以下の数値が相関係数です。応答値と設計変数の相関を示しています。
例えば、 「変数W、変数B」と「トルク平均値」の相関係数は絶対値が大きく、強い正の相関を持つことを示します。「変数W、変数B」は永久磁石の寸法です。永久磁石の体積の増加に伴いトルク平均値が大きくなることは容易に想像できます。この結果により最適化計算の結果が妥当であると判断できます。また、「変数X」と「トルクリップル」に着目すると負の相関を示しており、円筒状の空気領域がステータへ近づく程にトルクリップルが小さくなることが分かります。相関行列の表示画面では、相関係数以外にも対角項にヒストグラム、左下に散布図が示されています。
応答グラフ
応答グラフの一例として「変数A」と「変数S」の応答グラフを図9に示します。
「応答値：トルク平均値」の応答グラフは「トルク平均値－変数A」平面にて単調増加です。「 応答値：トルクリップル」 の応答グラフでは、「変数A」が小さい時と大きい時で極小値を2つ持ってると予想されます。 「変数A」と「変数S」のみで考える場合は、「変数A」を最大にすれば「トルク平均値の最大化」と「トルクリップルの最小化」の目的に対していいとこ取りできることが分かります。「変数A」を最大にした時の「変数S」に関しては、どちらの目的を優先するかによって3～5あたりで調整することになります。
