樹脂成形とレオロジー 第 9 回「 指数則流体の特性式」
純粘性流体の構成方程式
純粘性流体を対象とする場合は、応力とひずみ速度の量的関係を表す式を構成方程式(Constitutive equation)またはレオロジー方程式(Rheology Equation)とよびます。これを次式に示します。

ニュートン流体の場合、温度や圧力が一定ならηは定数となります。したがって、せん断速度とせん断応力の関係は線形になります。一方、プラスチックなどの溶融体では非線形になり、この特性を持つ物質を総称して非ニュートン流体といいます。
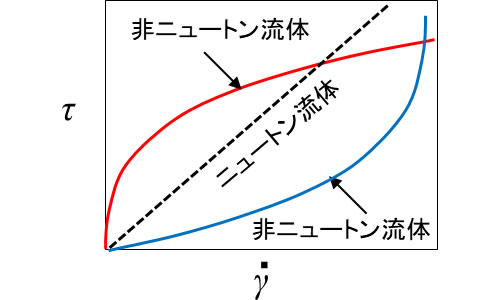
指数則モデル
せん断速度とせん断応力の関係を対数で表示したときの傾きが構造粘度指数 n となります。
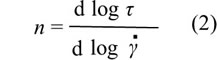
nが一定とみなせる領域で(2)式を積分すると κ を定数として次式が得られます。 κ は擬塑性粘度とよばれます。
![]()
(1)式、(3)式から次の関係が得られます。
![]()
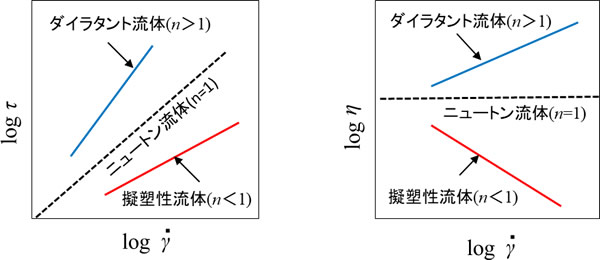
(3)式、(4)式で表わされる粘度モデルを指数則モデルやべき乗則(power law)モデルといいます。 n <1が擬塑性流体、 n =1がニュートン流体、 n >1がダイラタント流体とよばれています。溶融プラスチックの場合は n <1となる擬塑性流体としての特性を示す場合がほとんどです。
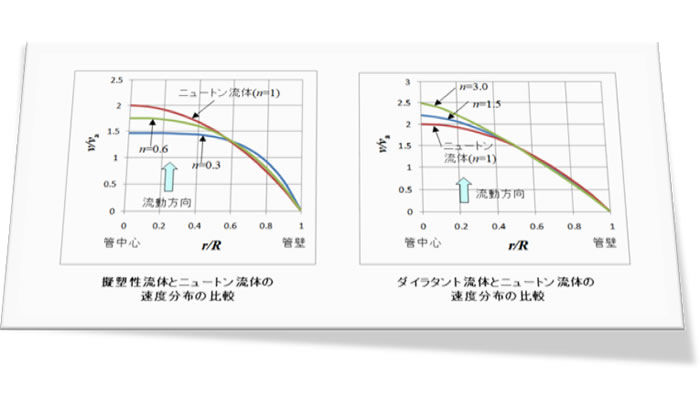
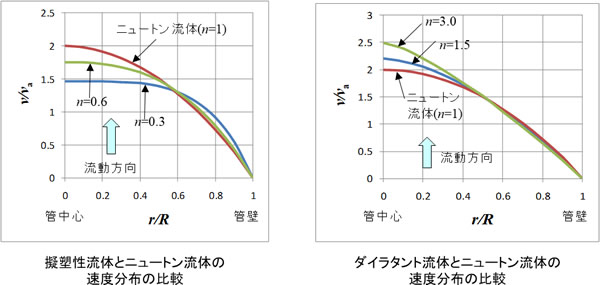
速度分布の比較
いま、同じ半径の一本の円管内を等温の非圧縮性流体が定常層流で流動し、管壁ですべりがなく、重力などの体積力が働かないと仮定します。この前提でのニュートン流体の運動方程式の厳密解はハーゲンポアゼイユ流れ(Hagen-Poiseuille flow)として流体力学の教科書に必ず記載されています。指数則モデルでも同様の手順で厳密解を求めることができます。無次元速度は次の形になります。

(5)式で n=1とおくと放物線の速度分布を持つハーゲンポアゼイユ流れと一致します。擬塑性流体(n<1)ではせん断速度の大きい管壁付近で粘度が低下するので、ニュートン流体に比べ抵抗が小さく流れが速くなります。一方、せん断速度の小さい菅中心付近では粘度が高くなるので、ニュートン流体よりも抵抗が大きくなり速度が遅くなります。ダイラタント流体(n>1)では逆に管壁付近で粘度が高くなるのでニュートン流体に比べ速度が遅くなり、管中心付近で粘度が低下するのでニュートン流体よりも速度が速くなります。
※関連記事:OpenFOAMの粘性モデル
関連記事/関連ページ