Mat. Curve Modeller:
遅れて来たもう一つの材料データ作成ツール – 8
最適化ツールの機能の向上と相まって、非線形材料データの作成方法、検証方法は多くの研究者、企業からの提案があり、商品化もされています。弊社でも、独自の視点を形にした材料データ作成ソフトMat. Curve Modellerを2021年11月にリリースしました。以下に、開発者によるコラムをお届けします。

前回まで、のべ3回にわたってMat. Curve Modeller のMises⇔SAMP変換機能に焦点をあて、単軸引張変形及び単軸圧縮変形(以下、単軸変形に省略)における弾塑性を考慮した真応力を導出しました。ところで、SAMPモデルでは、樹脂材料の2軸引張特性を考慮することが可能です。樹脂材料は2軸引張変形によって白化しやすくなる(壊れやすくなる)と議論されることがあるため、2軸引張変形を検討することも重要です。そこで、今回から2回にわけて、等方性材料の等2軸引張変形及び等2軸圧縮変形(以下、等2軸変形に省略)における弾塑性を考慮した真応力を導出し、Mises⇔SAMP変換機能(※)が等2軸変形にも対応していることを示します。
※ Mises⇔SAMP変換機能:Mises構成則用に作成された応力-ひずみ関係を、SAMP構成則用の応力-ひずみ関係に変換する機能。数学的な取り扱いについては、当コラム「 Mat. Curve Modeller:遅れて来たもう一つの材料データ作成ツール 」の第5回~第7回をご覧ください。
等2軸変形の真応力
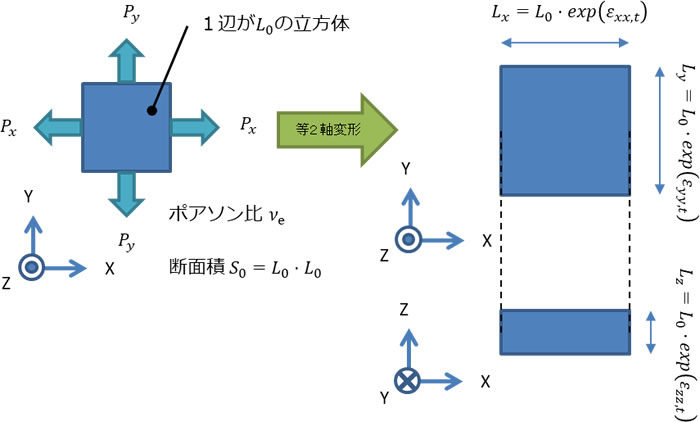
図1に示すように、これまで同様に1辺が \(L_{0}\) の立方体を変形させることを考えます。等方性材料を考えていますので、X、Y方向に等しい荷重 \(P_{x}\) , \(P_{y}\) を作用させ、X、Y方向に等しい真ひずみ \(\varepsilon_{xx,t}\) , \(\varepsilon_{yy,t}\) が生じることを前提とします。板厚方向のひずみが \(\varepsilon_{zz,t}\) です。
本コラム第5回の式5と同様に考えれば、変形後のYZ断面の断面積S(XZ断面の断面積と同じ値)は式(1)のように表せます。したがって、真応力は式(2)のようにあらわせます。ここで、導出を終わりにしても良いのですが、もう少しすっきりとした形式に書き換えることを考えてみましょう。

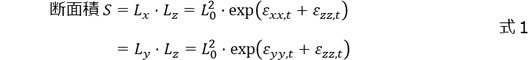
![]()
等2軸ポアソン比の導出
等2軸変形のひずみを真応力 \(\sigma_{xx}\) , \(\sigma_{yy}\) , \(\sigma_{zz}\) を用いて考えてみましょう。これは数々の教科書に載っていることなので、式だけを示します(式3)。もちろん、Z方向の応力はゼロです。ここで、添え字 u は1軸変形時の物性値を表します。 \(E_{u}\) は1軸変形時に得られる「応力-ひずみ」関係における弾性範囲の傾きです。
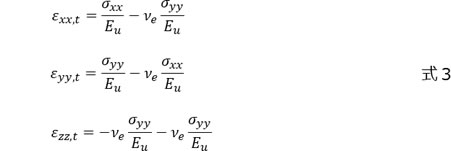
等2軸変形なので、X、Y方向の真応力、真ひずみは等しいです。このため、式3は式4のように書き直せます。
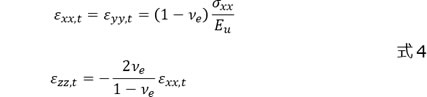
式4から式5を定義します。等2軸変形の「応力 \(\sigma_{xx}\) -ひずみ \(\varepsilon_{xx}\) 」関係における弾性範囲の傾きが 式5に示す \(E_{b}\) 、式6が等2軸変形時のポアソン比 \(\mu{_e}=-\frac{\varepsilon_{zz,t}}{\varepsilon_{xx,t}}\) です。
![]()
![]()
したがって、式2は式6を利用して、すっきりとした形に書き直せます。非圧縮変形の場合、ポアソン比 \(\nu{_e}\) は0.5なので、等2軸ポアソン比 \(\mu{_e}\) は2です。式7は式8のようにあらわせます。単軸変形時の真応力と同じ形の式になります。
![]()
![]()
等2軸変形時の相当ひずみ
最後に、等2軸変形における相当ひずみを確認してみましょう。式9に等2軸変形における相当ひずみを示します。ここで、ポアソン比 \(\nu{_e}\) は0.5としています。さらに、単軸変形における相当ひずみを式10に示します。ともに、X方向の真ひずみだけで表せますが、等2軸変形の相当ひずみはX方向の真ひずみの2倍、単軸変形における相当ひずみはX方向の真ひずみと等しい、ということが示されています。
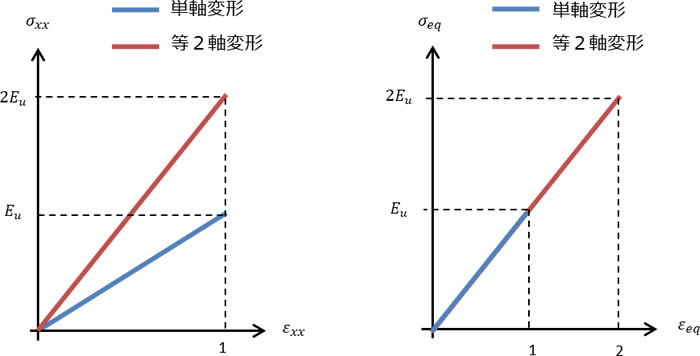
これらの結果を理解するには、応力-ひずみ関係(SSカーブ)を確認すると良いです。図2にSSカーブを示します。右は横軸を相当ひずみ基準でSSカーブをプロットした結果、左は横軸を真ひずみ基準でSSカーブをプロットした結果です。相当ひずみ基準のグラフでは、縦軸を相当応力(ここでは、ミーゼス応力 \(\sigma_{eq}\) に変換しています。真ひずみ基準では、2軸変形の方が硬いと解釈できます。相当ひずみ基準では両者は重なります。試験方法が異なるので、真ひずみ基準で比較することは適切ではなく、相当ひずみで比較することが望ましいでしょう。
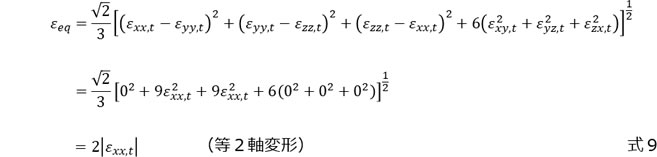
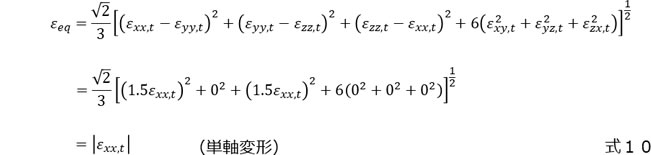
![]()
塑性変形を伴うときの真応力
2軸変形と聞くと難しく思えてしまいますが、等方性材料かつ等2軸変形であれば簡単に考えることができます。次回は、弾塑性変形時の等2軸真応力を導出します。
関連ページ/参考文献
竹越、丹羽、” MAT_SAMP-1樹脂材料データ作成技術の紹介”、LS-DYNA & JSTAMP Forum 2013 JSOL.
竹越、”塑性体積膨張を示す樹脂の材料データ作成手法の検討”、第57回日本学術会議材料工学連合講演会 日本材料学会 7
●Mat. Curve Modeller:遅れて来たもう一つの材料データ作成ツール – 7
●Mat. Curve Modeller:遅れて来たもう一つの材料データ作成ツール – 9
●Mat.Curve Modellerのページ
