樹脂成形とレオロジー第37回「キャピラリー押出粘度計」

これまで色々な粘度モデルをご紹介してきましたが、これからしばらくは粘度の測定法を取り上げたいと思います。なお、ここで使う粘度はせん断速度とせん断応力の比例定数であるせん断粘度とします。粘度は試料にせん断速度を与えたときに壁で受ける力を基にして計算されます。せん断速度の与え方が異なる多くのタイプの粘度計が存在します。ここではまず、樹脂粘度の測定でもっともよく用いられているキャピラリー押出粘度計の原理を説明します。
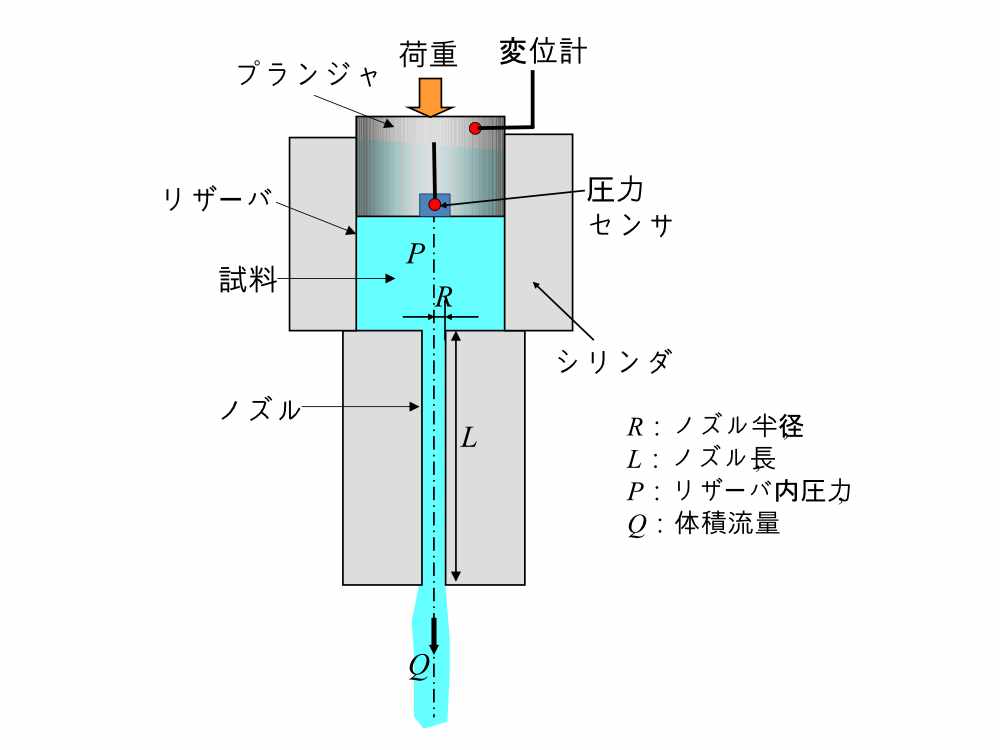
図1にキャピラリー押出粘度計の断面の概略を示します。この粘度計は金型、駆動部、センサ部、データ記録部から構成されています。金型はリザーバとよばれる中空部分を持つシリンダと細いノズル(キャピラリー)を設けた部分からなります。シリンダにはヒータなどの加熱手段が設けられており、所望の温度に設定できます。ノズル部は交換可能であり、ノズルの径や長さを変えて実験ができます。測定時には所定量の樹脂をリザーバに投入し、一定温度になるまで放置します。所定時間経過後、プランジャを押し下げ、リザーバ内の樹脂はノズルに流入し、ノズル端から大気圧中に解放されます。このときにプランジャの位置と時間の関係が記録されます。荷重とリザーバ径、ノズルの諸元、プランジャの降下速度ならびにリザーバ内の圧力指示値から、まず、ニュートン流体と仮定したときの見かけ粘度が計算できます。ただし、粘弾性性質の大きい高分子溶融体の場合は、リザーバからノズルに流入する際の付加圧力損失が生じること、ならびに非ニュートン流体としてのレオロジー特性値を正確に求める必要があることから、ノズルの長さと径の組合せなどを変え、所定の解析方法で各種誤差を補正することが必要となります。
この粘度計の特徴は荷重とノズル諸元の組合せにより広範囲のせん断速度領域での測定が可能なことです。実際の射出成形のゲート部で生じる高せん断速度も得ることができ、実成形との対応がつきやすい利点があります。また、ノズル端から樹脂が流出するので、Die Swellやメルトフラクチャなどの高分子溶融体特有の現象も観察可能です。
![]()
見かけ粘度の求め方
ここでは以下の前提を設けます。
①リザーバ径はノズル径に比べて非常に大きく試料がリザーバ内を流動中の圧力損失は無視する。
②ノズル外部は大気圧であり、リザーバ内の圧力Pは大気圧をキャンセルしたゲージ圧とする。
③試料の粘弾性性質に起因するリザーバからノズル内に流入するときの付加圧力損失を無視する。
④ノズル内をニュートン流体が等温、定常、層流状態で流動する。
圧力により試料をノズル内に押し込む力とノズル壁で受け止める力が釣り合うので次式が成立します。
$$
\pi R^{2} P = 2 \pi R L \tau_{W}^{\prime}
\qquad\text{・・・・・・・(1)}
$$
ここで、\(P\):リザーバ内圧力、\(R\):ノズル半径、\(L\):ノズル長さ、\(\tau_{W}’\):見かけの管壁せん断応力です。(1)式から\(\tau_{W}’\)は次式で求められます。
$$
\tau_{W}^{\prime} = \frac{P R}{2 L}
\qquad\text{・・・・・・・(2)}
$$
円管内の運動方程式の解から見かけの管壁せん断速度は次式となります。
$$
\dot{\gamma}_{W}^{\prime} = \frac{4 Q}{\pi R^{3}}
\qquad\text{・・・・・・・(3)}
$$
ここで、\(\dot{\gamma}_{W}’\):見かけの管壁せん断速度、\(Q\):体積流量です。したがって見かけの粘度は次式となります。
$$
\eta_{a}
= \frac{\tau_{W}^{\prime}}{\dot{\gamma}_{W}^{\prime}}
= \frac{\pi P R^{4}}{8 Q L}
\qquad\text{・・・・・・・(4)}
$$
ここで、\(\eta_a\):見かけの粘度です。ここに示した手順はせん断応力やせん断速度、粘度のおよその値を知るのに便利です。しかし、実際の溶融樹脂は粘弾性性質を持った非ニュートン流体ですので前提の③,④は成立しません。CAE用粘度モデル式に正確に当てはめるためには次に示す真粘度を求める手順が必要になります。
真粘度の求め方
樹脂のような高分子溶融体では粘弾性性質によりリザーバからノズルに入るときに付加圧力損失を生じます。すなわち、リザーバ内の圧力\(P\)の一部はその仕事に消費され、ノズル入り口に加わる実際の圧力はそれよりも小さくなります。したがって実際のせん断応力は(2)式よりも小さくなります。このとき、圧力\(P\)はそのままにしておいて、ノズル長が伸びたとみなす方法がよく用いられます。すなわち、(2)式の分子の\(P\)を小さくする代わりにこれに相当する分だけ分母の\(L\)を長くして真のせん断応力を求めるという方法です。これを次式に示します。
$$
\tau_{W} = \frac{P R}{2\left(L + \nu R\right)}
\qquad\text{・・・・・・・(5)}
$$
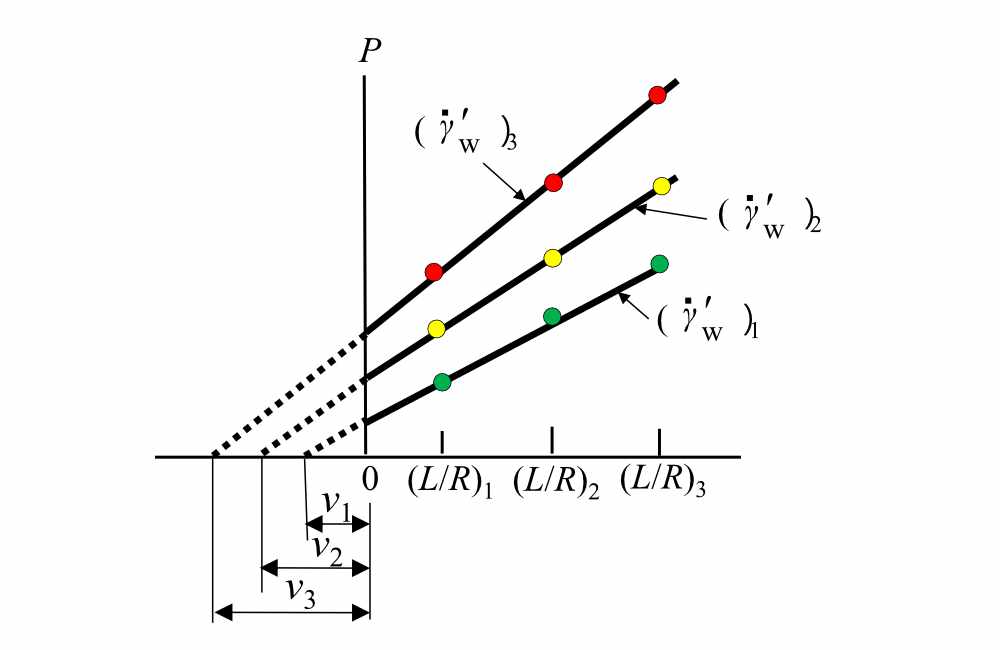
ここで、\(\tau_{W}\):真の管壁せん断応力、 \(\nu\) :管長補正係数です。実験ではプランジャ荷重とノズルの \(L/R\) の比率を変えた実験を行い、多くの \(\dot{\gamma}_{W}’\) のデータを取得し、\(P\) と \(L/R\) の関係のグラフ上で各 \(\dot{\gamma}_{W}’\) ごとに線を引きます。これを図2に示します。\(L/R = 0\) のところで圧力 \(P\) は 0 にならず、この圧力が付加圧力損失を示しています。そして各 \(\dot{\gamma}_{W}’\) のラインを\(L/R\) の負の側に延長し、\(L/R\) 軸の切片のところの絶対値が各 \(\dot{\gamma}_{W}’\) における管長補正係数 \(\nu\) となります。この手法を Bagley の管長補正といい、図2のグラフは Bagley’s plot とよばれています。
![]()
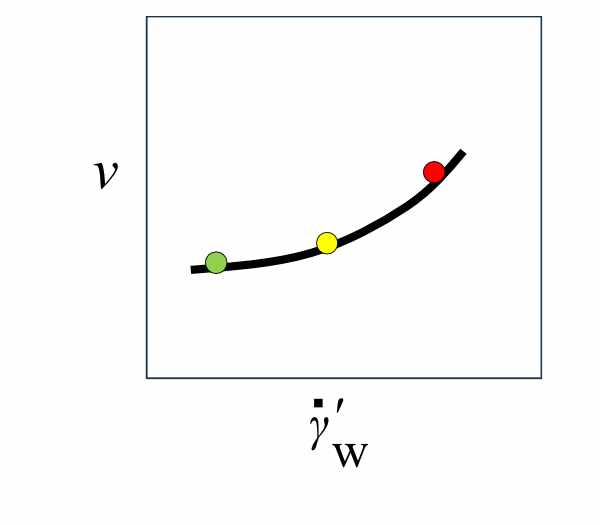
図2から図3のグラフが得られます。実験で得られた \(\dot{\gamma}_{W}’\) に対応する \(\nu\) を読み取り、(5)式で \(\tau_{W}\) を計算します。
![]()
一方、非ニュートン性を考慮 したときの真の管壁せん断速度は下式で求められます。これは等温、定常、層流の流体の運動方程式から理論的に導かれたものでRabinowitsch(ラビノビッチ)補正とよばれています。指数則流体の場合、次式となります。
$$
\dot{\gamma}_{W}
= \left(\frac{3n + 1}{4n}\right)\dot{\gamma}_{W}^{\prime}
\qquad\text{・・・・・・・(6)}
$$
ここで、\(\dot{\gamma}_{W}\):真の管壁せん断速度、\(n\):構造粘度指数、\(\dot{\gamma}_{W}’\):見かけの管壁せん断速度です。指数則流体以外の非ニュートン流体に対しては次式を適用します。
$$
\dot{\gamma}_{W}
= \left(
\frac{3}{4}
+ \frac{1}{4}
\frac{d \log \left(\dot{\gamma}_{W}^{\prime}\right)}
{d \log \left(\tau_{W}\right)}
\right)
\dot{\gamma}_{W}^{\prime}
\qquad\text{・・・・・・・(7)}
$$
真粘度は次式で求められます。
$$
\eta = \frac{\tau_{W}}{\dot{\gamma}_{W}}
\qquad\text{・・・・・・・(8)}
$$
ここで、\(\eta\):真粘度です。なお、真粘度の求め方の詳細手順の説明や補正方法の実習、ならびに別の補正方法の紹介などは弊社「樹脂流動解析スキルアップセミナー」で行っております。
関連記事/関連ページ
