解析内容
．磁界－構造連成解析（一方向連成）を用いて、IPMモータの寸法最適化を行った事例を紹介します。本事例では、IPMモータの2次元磁界過渡応答解析を実施し、各部品に作用する電磁力を算出します。得られた電磁力を荷重条件として2次元構造過渡応答解析を行い、ロータに発生する応力を算出します。さらに、以下の3項目を目標として最適化計算を実施します。
- トルク平均値の最大化
- トルクリップルの最小化
- ロータにかかる応力の120MPa以下
解析モデル
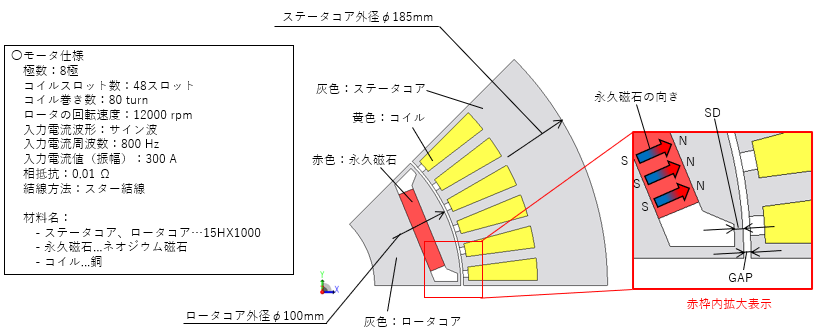
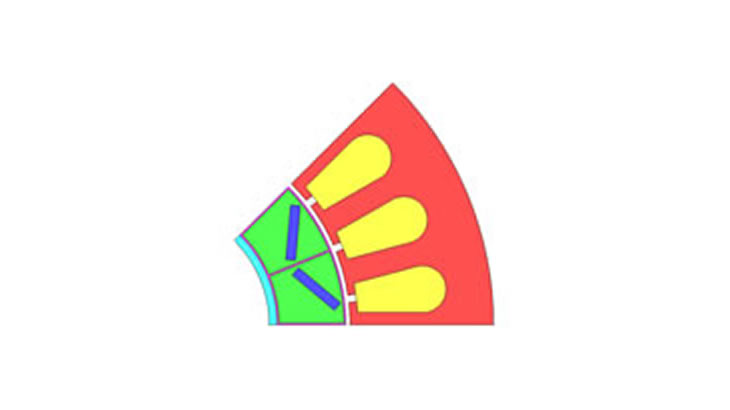
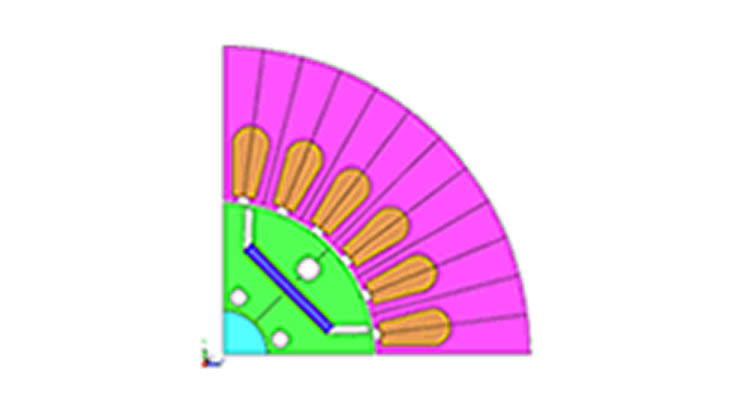
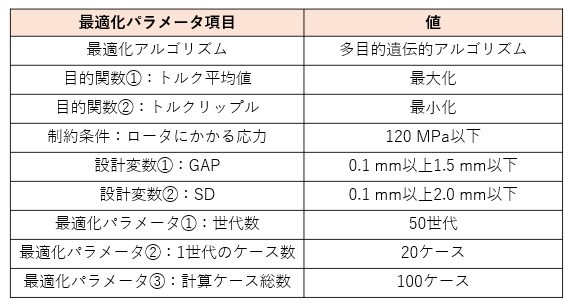
．モデル概要図を図1に示します。対称性を考慮して1/8対称（反周期境界）でモデル化します。最適化パラメータ一覧を表1に示します。
図1：モデル概要図（積層厚さ100 mm、占積率98%）
表1：最適化パラメータ一覧
解析結果
〇解分布
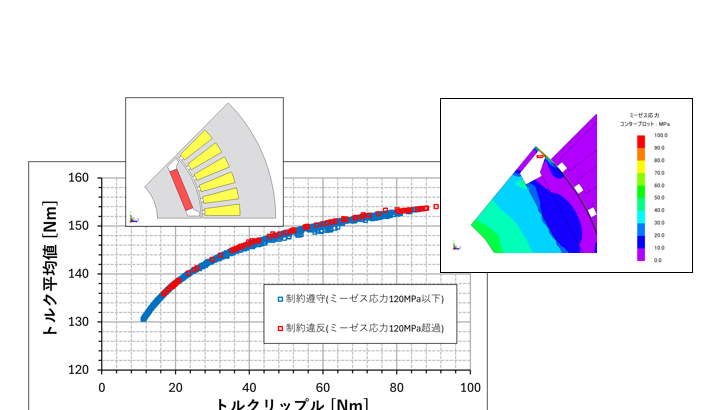
．全世代の解のうち制約条件「ロータにかかる応力が120 MPa以下」を満たす解分布を図2に示します。本事例では、トルク平均値とトルクリップルはトレードオフな関係であることが分かります。
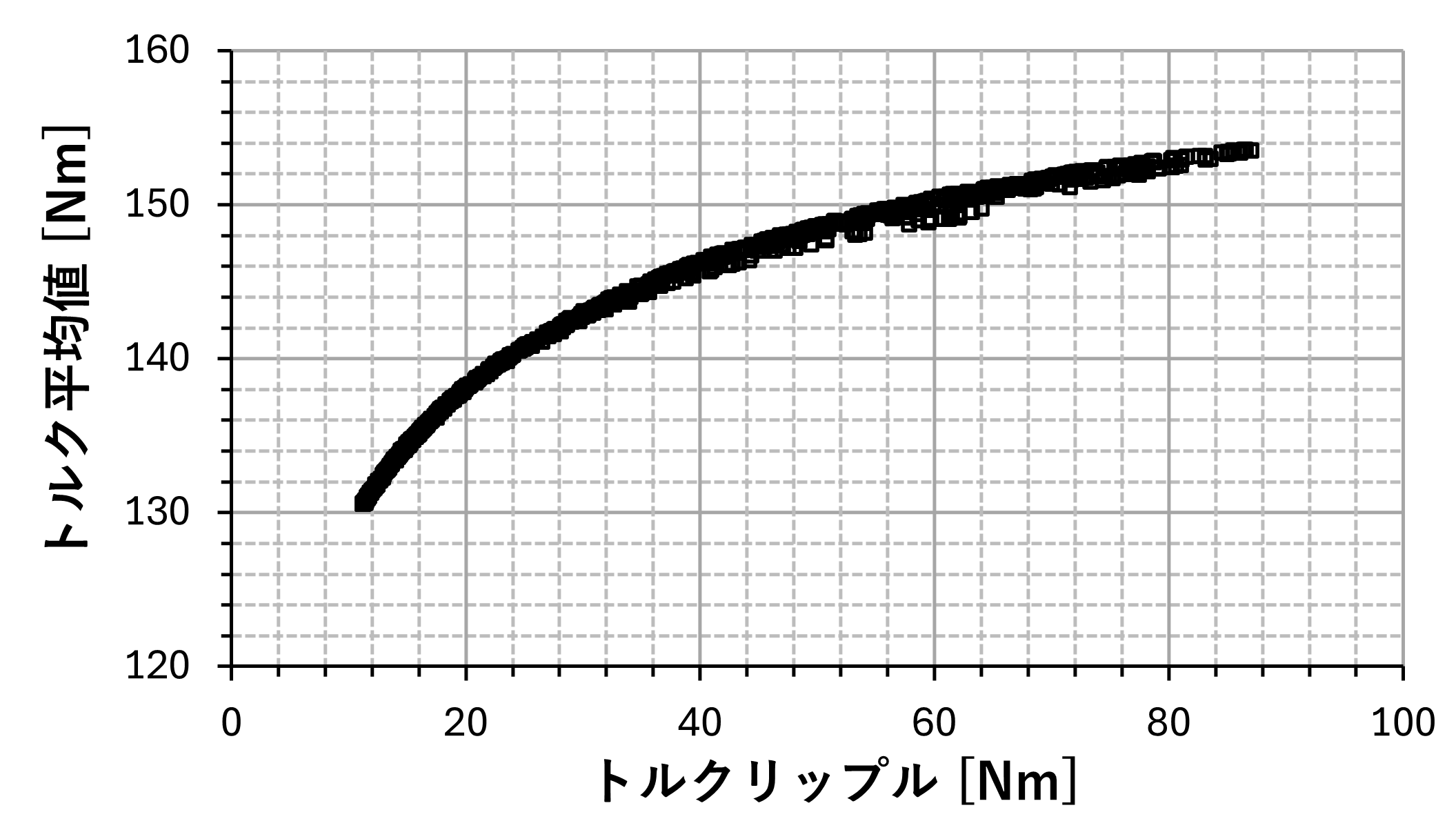
図2：最適化計算の解分布
〇各目的関数および制約条件の設計変数依存性
．各目的関数および制約条件の設計変数依存性を図3に示します。トルク平均値およびトルクリップルはSDよりGAPに依存しており、一方、ミーゼス応力はGAPよりSDに依存しています。どの寸法がどの結果に影響するか知ることで、効率よく設計することが可能です。今回は2つの設計変数で計算していますが、設計変数を増やすことでより多くの知見を得ることができます。
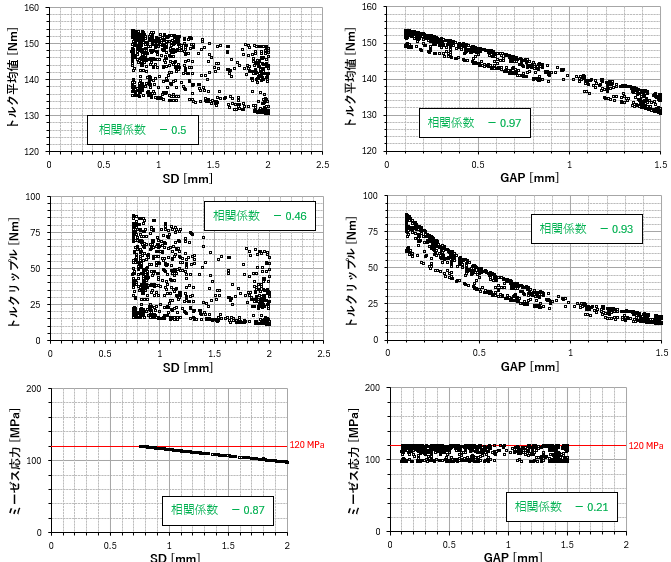
図3：各目的関数および制約条件の設計変数依存性（縦軸：目的関数および制約条件、横軸：設計変数）
〇代表ケースの計算結果
．解分布のうち特定の解の詳細も確認可能です。制約条件を満たす解のうち、トルク平均値が最大となった解を代表ケース①、トルクリップルが最小となった解を代表ケース②とします。代表ケース①と代表ケース②の解分布上の位置を図4に示します。各代表ケースのトルク波形を図5に示します。各代表ケースにおけるミーゼス応力最大値発生時のミーゼス応力分布を図６と図7に示します。代表ケース①と代表ケース②のミーゼス応力分布アニメーションをそれぞれ動画1と動画2に示します。
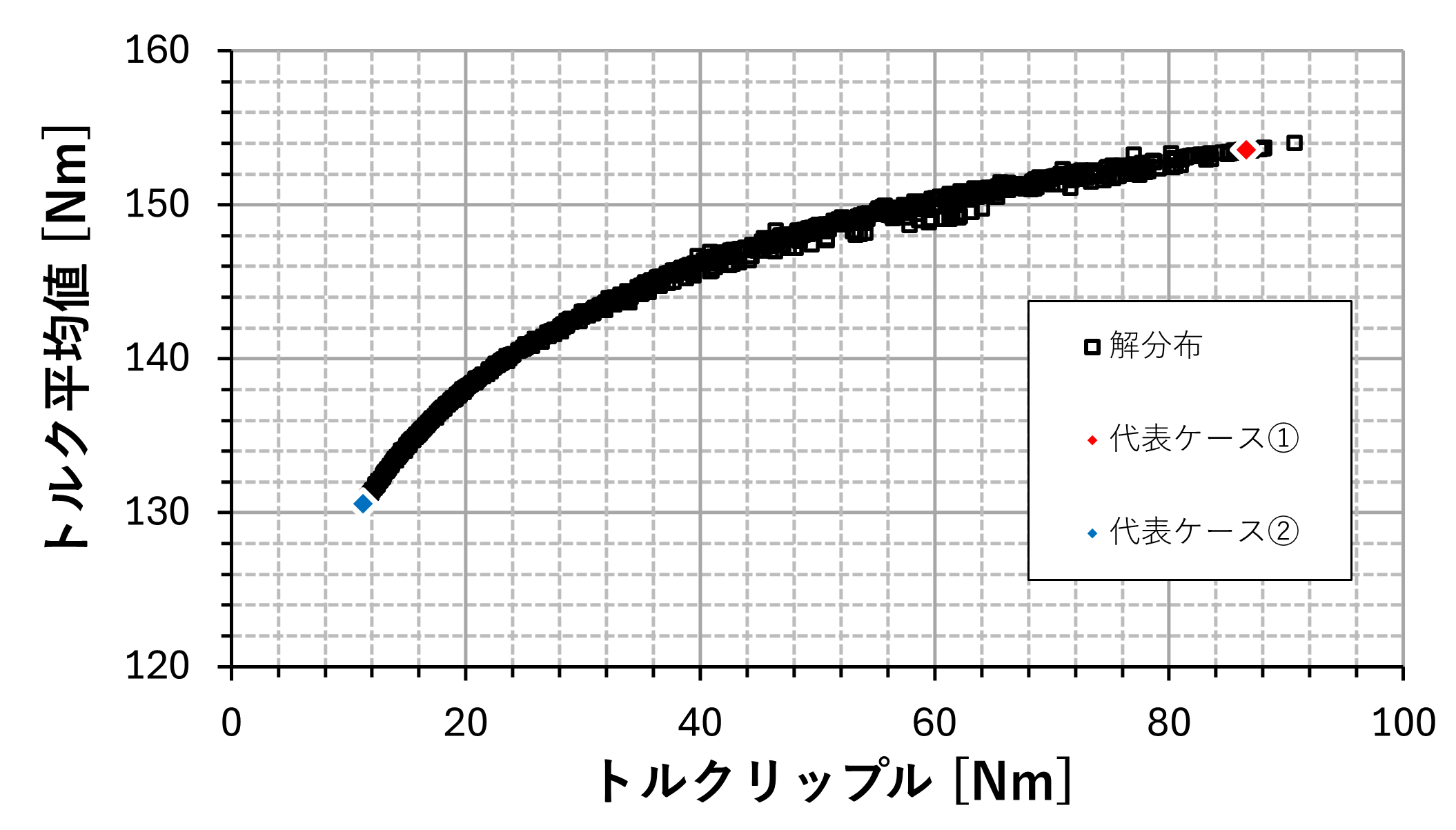図4：最適化計算の解分布における代表ケースの解の位置
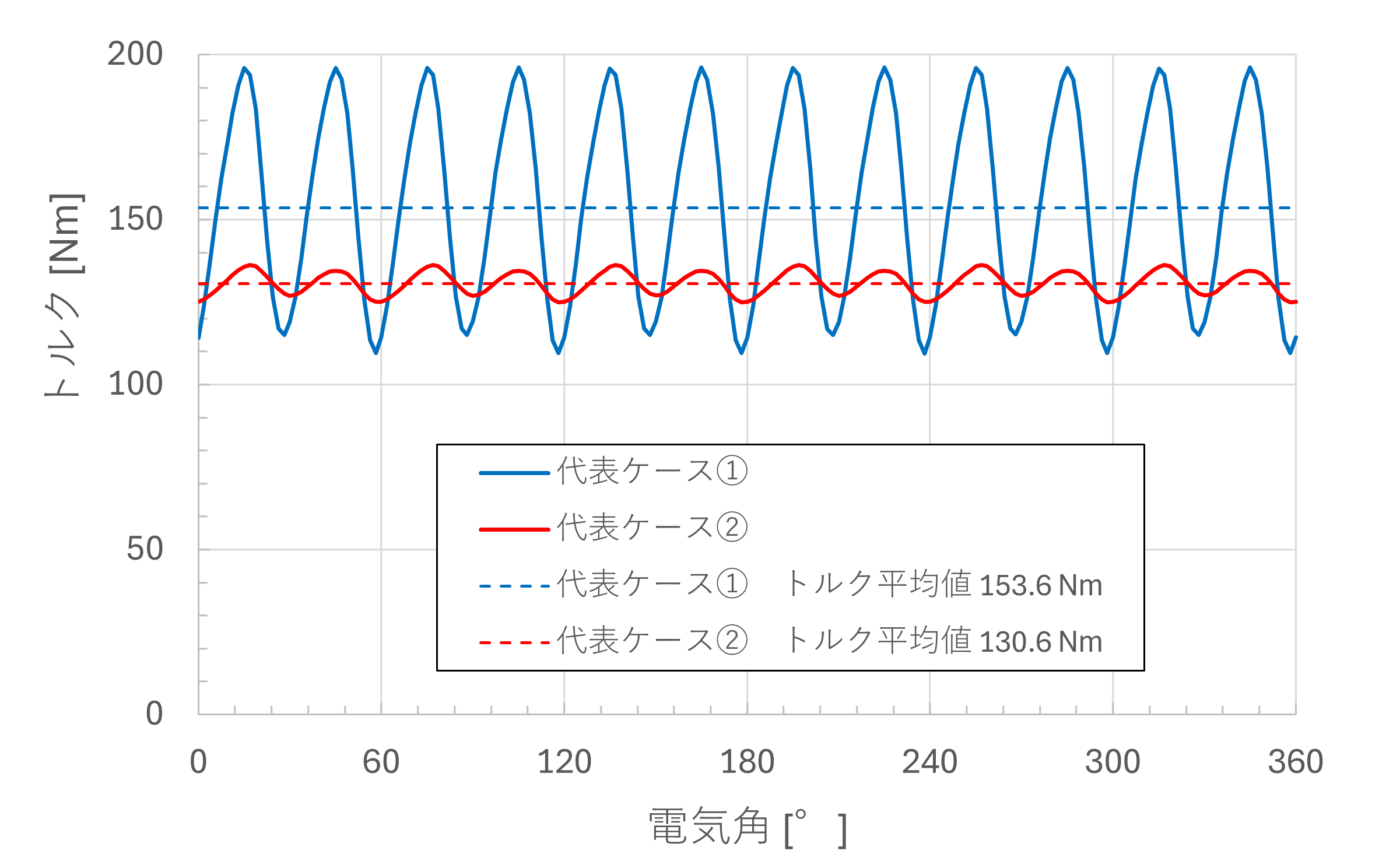図5：各代表ケースのトルク波形
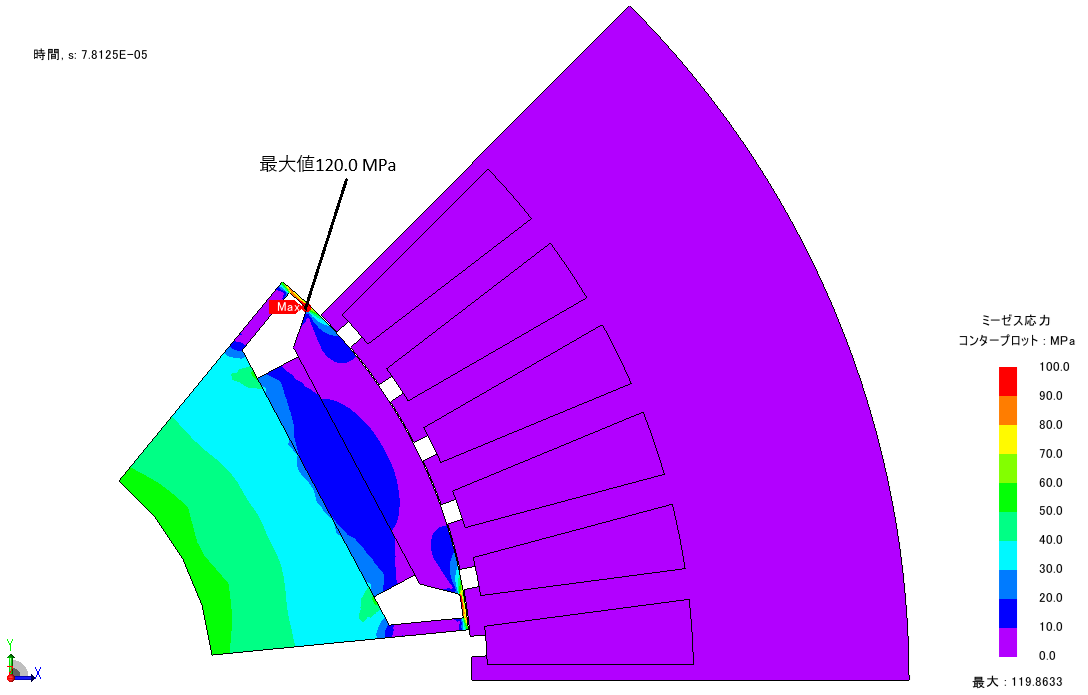
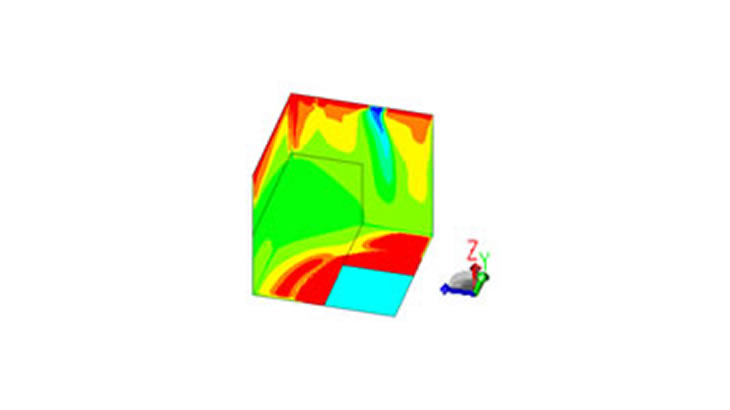
図6：代表ケース①の最大値発生時のミーゼス応力分布（電気角22.5°の時）
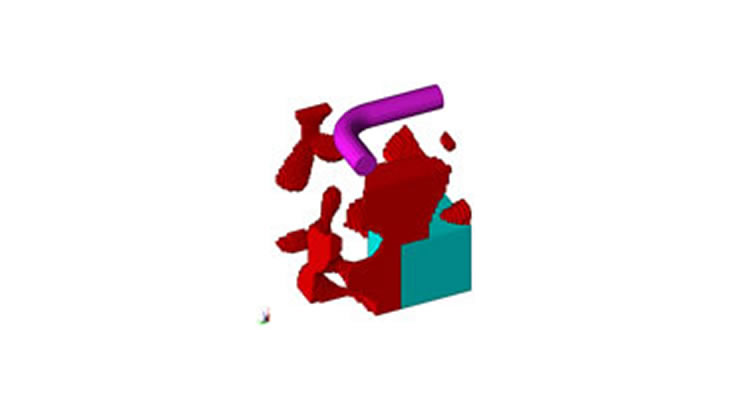
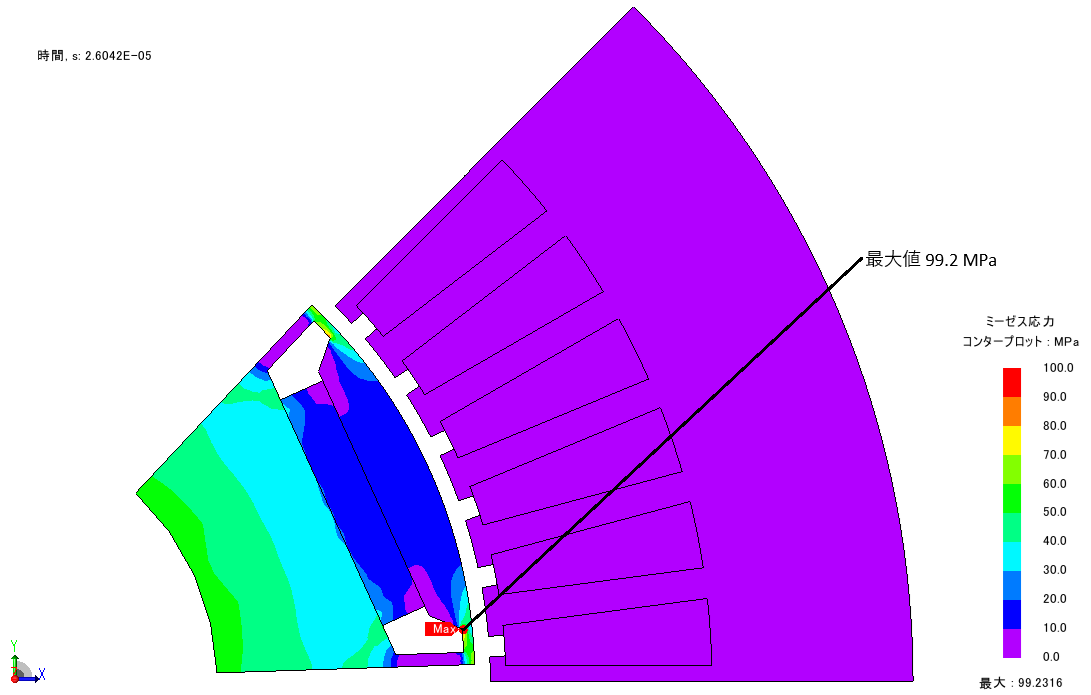図7：代表ケース②の最大値発生時のミーゼス応力分布（電気角7.5°の時）
動画1：代表ケース①のミーゼス応力分布アニメーション（1ティース分の回転角度）
動画2：代表ケース②のミーゼス応力分布アニメーション（1ティース分の回転角度）
