荷電粒子軌道解析 LORENTZ

ホーム > 電磁界解析 > INTGRATED電磁界ソフトウェア >製品情報 > LORENTZ
Trajectories in an Axial Magnetic Field Magnetron
Integrated Engineering Software
220 - 1821 Wellington Avenue, Winnipeg, Canada, R3H 0G4
ABSTRACT One of our benchmark problems for LORENTZ-3D is an axial magnetic field magnetron. This article demonstrates how LORENTZ-3D is able to solve electric and magnetic field solutions simultaneous, then track the trajectories of particles launched in those fields. The field and trajectory calculations are in very close agreement with the analytic solutions, and demonstrate particle trapping as a side-effect of the fringing of the fields in the geometry chosen. |
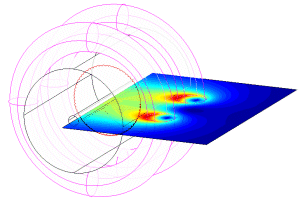
Magnetic Part
As shown in the image to the left, the magnetic part of the field was obtained using a Helmholtz Coil (click for a full size view). The Helmholtz Coil achieves a highly uniform magnetic field in a volume near the center (where the particles will be launched). This field is directed along the axis defining center of the two coils.
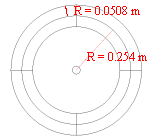 The chosen
The chosen
Helmholtz
Coils have:
radius = 0.254 m
current = 1 kA
For this case, the magnetic flux density at the center of an ideal
Helmholtz coil is:
B = uoI/[(5/4)3/2radius]
= 4*pi*10-7*1000 / [(5/4)3/2*0.254] = 0.03540 T = 35.40 G
Lorentz calculates a flux density at the center of 35.33 G - a difference of 0.2% owing to the thickness of the coils.
Electric Part
 The electric part of the field is setup using two cylindrical conductors sharing the same axis as the Helmholtz Coils.
The electric part of the field is setup using two cylindrical conductors sharing the same axis as the Helmholtz Coils.
Outer Cylinder
radius = 0.183 m (0.72 in)
length = 0.5715 m (22.5 in)
voltage = 0 V
Inner Cylinder
radius = 0.0183 m (0.72 in)
length = 0.5715 m (22.5 in)
voltage = 1000 V
The contour plot above shows voltage on a plane slicing through the two clyinders. The plot shows that inside the cylinders the voltage is quite uniform along the direction of the axis. As expected there are fringing effects at the ends of the cylinders.
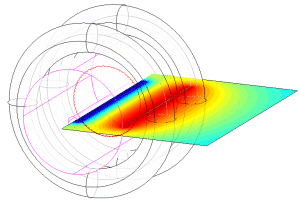
 Trajectories
Trajectories
The major contributions to the trajectory are the large orbit produced by the E/B drift of the guiding center, and the small oscillations at the cyclotron frequency. The particular orbit shown here was produced by releasing the electron from rest at a radius of 0.12 m. The electron is accelerated outwards by the electric field, but as it gains speed it has a Lorentz force of qvB. This force becomes larger the farther outwards the electron moves and eventually overcomes the electric force and causes the electron to loop back towards its original radius (but displaced by a small amount). There is a cusp at this point due to the electron coming to rest again momentarily.
| Extent of the E & B Values in the Trajectory | |||
|
Min | Max | Mean Value (STD) |
| r | 0.120 m | 0.1235 m | 0.12174 (0.0012) m |
| E | 3625 V/m | 3521 V/m | 3573 (37) V/m |
| B | 34.46 G | 34.34 G | 34.405 (0.041)G |
| Theoretical vs LORENTZ Values | |||
| Theoretical Value | LORENTZ Value | Discrepancy ** |
|
| Cyclotron Frequency | fc = qB/(2pi*m) = 96.31 MHz | 96.23 MHz | 0.08% |
| Magnetron Frequency | fm = v/(2pi*r) = E/(B*2pi*r) = 3573/(0.0034405 *2*pi*0.12174) = 1.358 MHz | 1.364 MHz | 0.43% |
** these discrepancy figures are provided to demonstrate the capability of Lorentz to output trajectories with the accuracy relative to a theoretical value limited by the fields themselves. For the cyclotron frequency only the magnetic field (standard deviation =0.1%) is important. For the magnetron frequency the electric field is the limiting factor (1% standard deviation). Note that although the field solver portion of LORENTZ provides the user with various ways of trading off solution accuracy versus computation time - the field variations observed here are due mainly to the differing radial positions during an orbit.
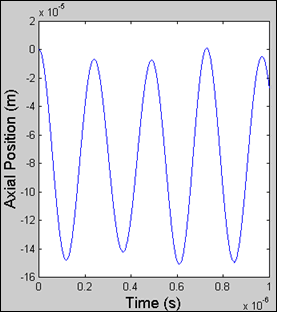
 The analyses have been chosen for an electron released from rest because this will generate the smallest radial motion, hence keep the field variations to a minumum for comparison with theory. However, this is a small subset of the general shape as shown to the right - oscillations about a guiding center while performing a larger orbit.
The analyses have been chosen for an electron released from rest because this will generate the smallest radial motion, hence keep the field variations to a minumum for comparison with theory. However, this is a small subset of the general shape as shown to the right - oscillations about a guiding center while performing a larger orbit.
Noise and Fringing Effects
 Any real device is not going to be as simple as a a radial E field and an axial B field. Finite size geometries mean that as soon as a particle strays off of a plane of symmetry, there will be other field components to be contended with. One of the benefits of simulation software such as LORENTZ is the ability to determine whether the fringing fields will lead to stability or not.
Any real device is not going to be as simple as a a radial E field and an axial B field. Finite size geometries mean that as soon as a particle strays off of a plane of symmetry, there will be other field components to be contended with. One of the benefits of simulation software such as LORENTZ is the ability to determine whether the fringing fields will lead to stability or not.
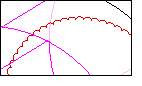
As seen to the left there are small axial oscillations at 4.12 MHz in the trajectory solution analyzed above. Small amounts of noise in the field solution (including zero axial force not quite corresponding to exactly the axial center) will cause the particle to start moving in an axial direction. Once the particle is off of the symmetric axis however, in this design the effect of both the E & B fringe fields is to push back towards the center (a simple harmonic oscillator in the axial direction).
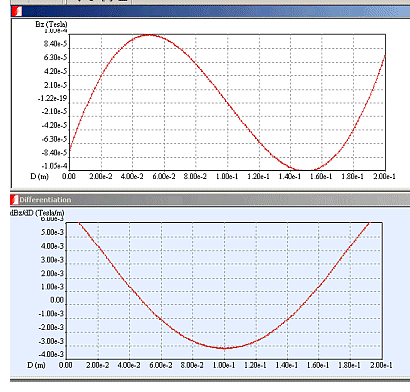 The plots to the right are found by following a straight line parallel to the axis at a separation of 0.1217 m. The line reaches the center at 0.1 m and the Bz component being plotted is the radial component of the B field. Treating the problem analogously to a mass on a spring, the spring constant is given by the charge times the cross product of the velocity with the gradient of the B field. Since there is tremendous variation in the speed of the electron, we use the net drift velocity, which is then perendicular to Bradial - giving rise to an axial force. From this we predict a frequency of 3.85 MHz for an electron near the center if we only allow for magnetic effects.
The plots to the right are found by following a straight line parallel to the axis at a separation of 0.1217 m. The line reaches the center at 0.1 m and the Bz component being plotted is the radial component of the B field. Treating the problem analogously to a mass on a spring, the spring constant is given by the charge times the cross product of the velocity with the gradient of the B field. Since there is tremendous variation in the speed of the electron, we use the net drift velocity, which is then perendicular to Bradial - giving rise to an axial force. From this we predict a frequency of 3.85 MHz for an electron near the center if we only allow for magnetic effects.
In the electrical case, there is again a net restoring force towards the center. The gradient in the axial component of the E field is 162 V/m2. This gives rise to a predicted frequency of 0.85 MHz if we only allow for electric effects.
Adding the electric and magnetic forces together to get a new spring constant, the predicted frequency becomes 3.94 MHz. However, this has all been done at the mean radius. To get an indication of the possible variations, we do the same at the outermost radius of the orbit and get 4.14 MHz. Hence, the observed 4.12 MHz is within the range of the frequencies that would be predicted by using the field solutions from different parts of the orbit.
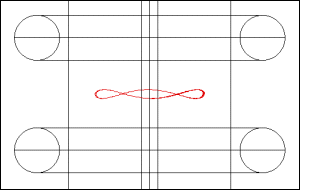 As seen above, the "spring constant" due to B decreases as the particle moves further away from the center. However, the "spring constant" for E increases and the two effects will cancel out to some extent. To the left is a screen shot of an orbit resulting from releasing the electron from rest at a radius of 0.12 m at a height of 0.01 m above the center. The observed frequency here is 4.10 MHz.
As seen above, the "spring constant" due to B decreases as the particle moves further away from the center. However, the "spring constant" for E increases and the two effects will cancel out to some extent. To the left is a screen shot of an orbit resulting from releasing the electron from rest at a radius of 0.12 m at a height of 0.01 m above the center. The observed frequency here is 4.10 MHz.
The fringing effects of the fields in the chosen geometry and release position for the electron are hence seen to act as a trap serving to confine the electron motion along the axis to a 4.1 MHz oscillation.
Copyright © 2009 Terrabyte Co.,Ltd.


